11 - A cravada de Deus e Inteiros¶

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

import pandas as pd

import networkx as nx
# from causalgraphicalmodels import CausalGraphicalModel

import arviz as az
# ArviZ ships with style sheets!
# https://python.arviz.org/en/stable/examples/styles.html#example-styles
az.style.use("arviz-darkgrid")

import xarray as xr

import stan
import nest_asyncio

plt.style.use('default')
plt.rcParams['axes.facecolor'] = 'lightgray'

# To DAG's
import daft
from causalgraphicalmodels import CausalGraphicalModel

# Add fonts to matplotlib to run xkcd

from matplotlib import font_manager

font_dirs = ["fonts/"]  # The path to the custom font file.
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)

for font_file in font_files:
    font_manager.fontManager.addfont(font_file)

# To make plots like drawing 
# plt.xkcd()

# To running the stan in jupyter notebook
nest_asyncio.apply()

R Code 11.1¶

df = pd.read_csv('./data/chimpanzees.csv', sep=';')
df.head()

	actor	recipient	block	trial	prosoc_left	chose_prosoc	pulled_left
0	1	NaN	1	2	0	1	0
1	1	NaN	1	4	0	0	1
2	1	NaN	1	6	1	0	0
3	1	NaN	1	8	0	1	0
4	1	NaN	1	10	1	1	1

pulled_left: Outcome \({0, 1}\) - indicator if the animal pulled the left-hand lever.
prosoc_left: Predict \({0, 1}\) - Indicator if left-hand lever was(1) or not(0) the prosocial options.
condition: Predict \({0, 1}\) - Indicator if there is a partner (1) or not (0) in the end table.

R Code 11.2¶

df['treatment'] = 1 + df['prosoc_left'] + 2 * df['condition']
df.head()

	actor	recipient	block	trial	prosoc_left	chose_prosoc	pulled_left	treatment
0	1	NaN	1	2	0	1	0	1
1	1	NaN	1	4	0	0	1	1
2	1	NaN	1	6	1	0	0	2
3	1	NaN	1	8	0	1	0	1
4	1	NaN	1	10	1	1	1	2

treatment= \(1\): prosoc_left = \(0\) and contition= \(0\): Two food items on right and no partner.
treatment= \(2\): prosoc_left = \(1\) and contition= \(0\): Two food items on left and no partner.
treatment= \(3\): prosoc_left = \(0\) and contition= \(1\): Two food items on right and has partner.
treatment= \(4\): prosoc_left = \(1\) and contition= \(1\): Two food items on left and has partner.

R Code 11.3¶

df.pivot_table(['prosoc_left', 'condition'], 'treatment', aggfunc='count', margins=True)

	condition	prosoc_left
treatment
1	126	126
2	126	126
3	126	126
4	126	126
All	504	504

def logit(p):
    return np.log(p) - np.log(1 - p)

def inv_logit(p):
    return np.exp(p) / (1 + np.exp(p))

\[ L_i \sim Binomial(1, p_i) \]

\[ logit(p_i) = \alpha_{ACTOR[i]} + \beta_{TREATEMENT[i]} \]

\[ \alpha_j \sim \mbox{to be determined} \]

\[ \beta_k \sim \mbox{to be determined} \]

Entendimento::

Likelihood:

Para esse caso os dados da resposta, outcome, são do tipo binários \(0\) ou \(1\). A função de likelihood apropriada para esses caso é a \(Bernoulli(p)\), ou no caso \(Binomial(1, p)\).

Como \(p\) é uma probabilidade, está entre \(0\) e \(1\), usamos uma função de ligação para transformar os resultados dos preditores para a escala de probabilidade. Nesse caso a função que faz essa transformação é:

\[ logit(p) = log(\frac{p}{1-p}) \]

Parameter \(\alpha\):

Na função de ligação o parâmetro \(\alpha\) é na verdade definido no modelo como um vetor (vector). O que estamos modelando aqui é que existe um parâmetro \(\alpha\) para cada chimpanzé, ou seja, para cada actor.

\[ \alpha[1] := \mbox{ Para o chimpanzé } 1 \]

\[ \alpha[2] := \mbox{ Para o chimpanzé } 2 \]

\[ \alpha[3] := \mbox{ Para o chimpanzé } 3 \]

\[ \alpha[4] := \mbox{ Para o chimpanzé } 4 \]

\[ \alpha[5] := \mbox{ Para o chimpanzé } 5 \]

\[ \alpha[6] := \mbox{ Para o chimpanzé } 6 \]

\[ \alpha[7] := \mbox{ Para o chimpanzé } 7 \]

Cada um dos parâmetros \(\alpha\) tem um priori \(Normal(\mu_i, \sigma_i)\) e essas prioris são idênticas.

O que estamos inferindo com cada um desses \(\alpha\)’s é a localização (\(\mu_i\)) de cada uma das prioris e seu desvio padrão (\(\sigma_i\))
Parameter \(\beta\):

O \(\beta\) é a representação de um vetor de \(\beta\)’s que mapeiam cada um dos tratamentos:

\[ \beta[1] := \mbox{ Para o tratamento } 1 \]

\[ \beta[2] := \mbox{ Para o tratamento } 2 \]

\[ \beta[3] := \mbox{ Para o tratamento } 3 \]

\[ \beta[4] := \mbox{ Para o tratamento } 4 \]

No experimento existe uma hipóstese a ser testada: Os chimpanzés tendem a puxar mais a alavanca do lado pro-social quando tem um outro chimpanzé do outro lado da mesa, o partner?

Os \(\alpha\)’s são independentes entre eles, porém quando colocamos os \(\beta\)’s estamos medindo qual é a inteção conjunta dos chimpanzés em cada tratamento.

A variável tratamento (treatment) é a construção de uma variável sintética que indexa o conjunto de duas variáveis {prosoc_left, condition}, isto é, a interação entre elas. Então temos que a variável \(treatment = 1\) indica que o experimento foi realizado usando dois pratos com comida no lado direito e que não tinha parceiro.

Portando \(\beta_{treatment = 1}\) terá o valor do efeito de todos os experimentos que os chimpanzés fizeram nesse tipo de tratamento.

R Code 11.4¶

\[ L_i \sim Binomial(1, p_i) \]

\[ logit(p_i) = \alpha \]

\[ \alpha \sim Normal(0, \omega) \]

\(\omega = 10\) to start

# Creating data list to model
data_list_partial = df[['pulled_left', 'actor']].to_dict('list')
data_list_partial['N'] = len(df)
data_list_partial['qty_chimpanzees'] = len(df.actor.unique())

data_list_partial.keys()

dict_keys(['pulled_left', 'actor', 'N', 'qty_chimpanzees'])

model_partial = """
    data {
        int N;
        int qty_chimpanzees;
        int pulled_left[N];
        int actor[N];
    }
    
    parameters {
        vector[qty_chimpanzees] alpha;
    }
    
    model {
        vector[N] p;
        
        // Prioris
        alpha ~ normal(0, 10);
        
        for (i in 1:N){
            p[i] = alpha[ actor[i] ];
            p[i] = inv_logit(p[i]);
        }
        
        // Likelihood
        pulled_left ~ binomial(1, p);
    }
"""

posteriori_partial = stan.build(model_partial, data=data_list_partial)
samples_partial = posteriori_partial.sample(num_chains=4, num_samples=1000)

az.summary(samples_partial, var_names=['alpha'], hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	-0.338	0.238	-0.688	0.063	0.004	0.003	3019.0	1984.0	1.0
alpha[1]	11.098	5.205	3.856	18.170	0.139	0.107	1828.0	1409.0	1.0
alpha[2]	-0.636	0.253	-1.034	-0.235	0.004	0.003	3580.0	2903.0	1.0
alpha[3]	-0.639	0.251	-1.040	-0.246	0.004	0.003	3621.0	2664.0	1.0
alpha[4]	-0.338	0.244	-0.722	0.066	0.004	0.003	3560.0	2618.0	1.0
alpha[5]	0.579	0.244	0.208	0.983	0.004	0.003	3508.0	2257.0	1.0
alpha[6]	2.141	0.392	1.495	2.730	0.007	0.005	3185.0	2189.0	1.0

samples_partial = az.from_pystan(
    posterior_model=posteriori_partial,
    posterior=samples_partial,
    observed_data=['pulled_left', 'actor']
)

R Code 11.5¶

# extract prior from quap
omega = 10
N = 1000

norm_prior = np.random.normal(0, omega, N)

R Code 11.6¶

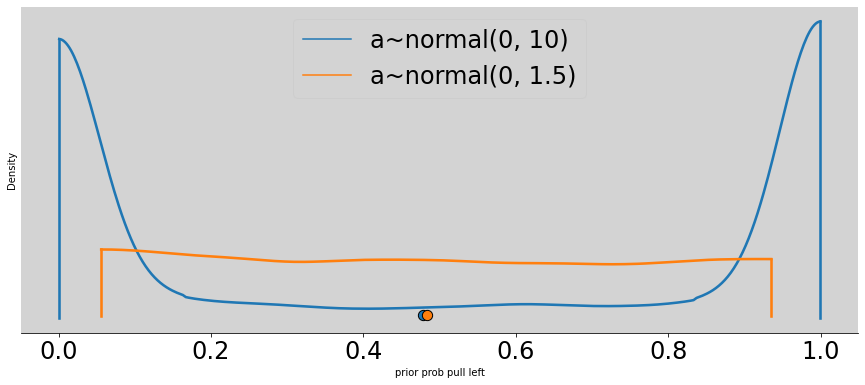
p = inv_logit(norm_prior)

omega = 1.5

better_p = inv_logit( np.random.normal(0, omega, N) ) 

az.plot_density([p, better_p],
                data_labels=['a~normal(0, 10)', 'a~normal(0, 1.5)'], 
                figsize=(15, 6))

plt.title('')
plt.xlabel('prior prob pull left')
plt.ylabel('Density')

plt.show()

model_partial_better = """
    data {
        int N;
        int qty_chimpanzees;
        int pulled_left[N];
        int actor[N];
    }
    
    parameters {
        vector[qty_chimpanzees] alpha;
    }
    
    model {
        vector[N] p;
        
        // Prioris
        alpha ~ normal(0, 1.5);
        
        for (i in 1:N){
            p[i] = alpha[ actor[i] ];
            p[i] = inv_logit(p[i]);
        }
        
        // Likelihood
        pulled_left ~ binomial(1, p);
    }
"""

posteriori_partial_better = stan.build(model_partial_better, data=data_list_partial)
samples_partial_better = posteriori_partial_better.sample(num_chains=4, num_samples=1000)

az.summary(samples_partial_better, var_names=['alpha'], hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	-0.335	0.230	-0.698	0.027	0.003	0.003	6221.0	3145.0	1.0
alpha[1]	3.926	0.733	2.836	5.104	0.011	0.009	4498.0	2492.0	1.0
alpha[2]	-0.623	0.247	-1.039	-0.242	0.003	0.002	7013.0	2992.0	1.0
alpha[3]	-0.625	0.254	-1.036	-0.229	0.003	0.002	6910.0	3005.0	1.0
alpha[4]	-0.331	0.232	-0.695	0.032	0.003	0.003	6917.0	2863.0	1.0
alpha[5]	0.563	0.243	0.187	0.954	0.003	0.003	5784.0	2874.0	1.0
alpha[6]	2.009	0.360	1.436	2.577	0.005	0.004	6087.0	2897.0	1.0

samples_parcial_better = az.from_pystan(
    posterior=samples_partial_better,
)

R Code 11.7¶

\[ L_i \sim Binomial(1, p_i) \]

\[ logit(p_i) = \alpha_{ACTOR[i]} + \beta_{TREATEMENT[i]} \]

\[ \alpha_j \sim Normal(0, 0.15) \]

\[ \beta_k \sim Normal(0, 10) \]

# quap code to get priori

R Code 11.8¶

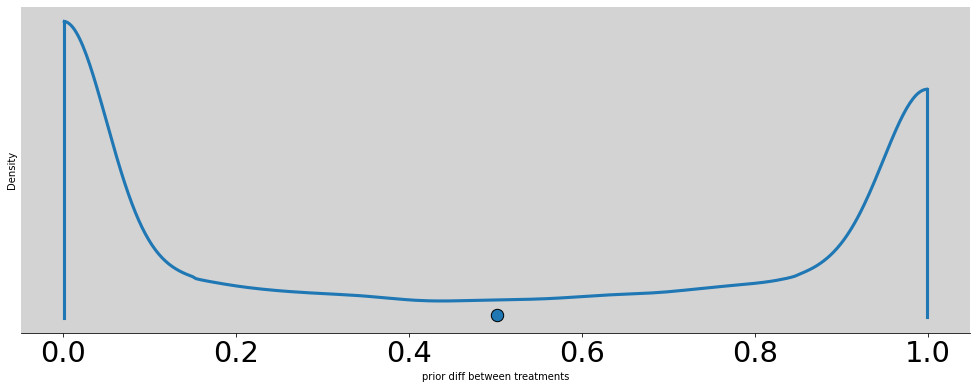
p = []

alpha = np.random.normal(0, 1.5, N)
betas = np.random.normal(0, 10, (4, N))

p = [inv_logit(alpha + beta) for beta in betas]

az.plot_density(np.absolute(p[0] - p[1]), figsize=(17, 6))

plt.title('')
plt.xlabel('prior diff between treatments')
plt.ylabel('Density')

plt.show()

R Code 11.9¶

\[ L_i \sim Binomial(1, p_i) \]

\[ logit(p_i) = \alpha_{ACTOR[i]} + \beta_{TREATEMENT[i]} \]

\[ \alpha_j \sim Normal(0, 0.15) \]

\[ \beta_k \sim Normal(0, 0.5) \]

better_p = []

alpha = np.random.normal(0, 1.5, N)
betas = np.random.normal(0, 0.5, (4, N))

better_p = [inv_logit(alpha + beta) for beta in betas]

az.plot_density([
        np.absolute(p[0] - p[1]), 
        np.absolute(better_p[0] - better_p[1])
    ], 
    data_labels=['b ~ normal(0, 10)', 'b ~ normal(0, 0.5)'],
    figsize=(15, 6))

plt.title('')
plt.xlabel('prior diff between treatments')
plt.ylabel('Density')

plt.show()

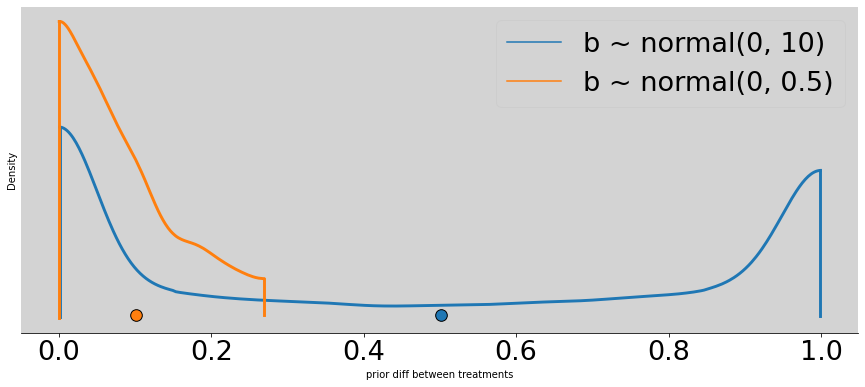
np.mean(np.absolute(better_p[0] - better_p[1]))

0.10040888662896558

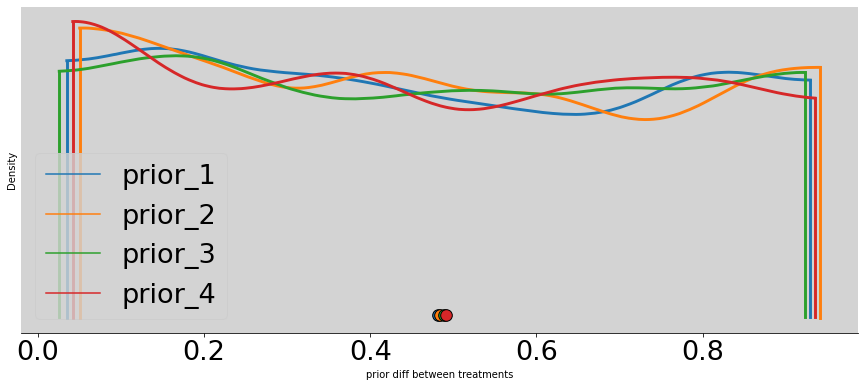
# Plot the 4 prior

az.plot_density([
        better_p[0], 
        better_p[1], 
        better_p[2], 
        better_p[3], 
    ],
    data_labels=['prior_1', 'prior_2', 'prior_3', 'prior_4'], 
    figsize=(15, 6))

plt.title('')
plt.xlabel('prior diff between treatments')
plt.ylabel('Density')

plt.show()

R Code 11.10¶

data_list = df[['pulled_left', 'actor', 'treatment']].to_dict('list')
data_list['N'] = len(df)
data_list['qty_chimpanzees'] = len(df.actor.unique())
data_list['qty_treatment'] = len(df.treatment.unique())

data_list.keys()

dict_keys(['pulled_left', 'actor', 'treatment', 'N', 'qty_chimpanzees', 'qty_treatment'])

R Code 11.11¶

model = """
    data {
        int N;
        int qty_chimpanzees;
        int qty_treatment;
        int pulled_left[N];
        int actor[N];
        int treatment[N];
    }
    
    parameters {
        vector[qty_chimpanzees] alpha;
        vector[qty_treatment] beta;
    }
    
    model {
        vector[N] p;
        
        // Prioris
        alpha ~ normal(0, 1.5);
        beta ~ normal(0, 0.5);
        
        for (i in 1:N){
            p[i] = alpha[ actor[i] ] + beta[ treatment[i] ];
            p[i] = inv_logit(p[i]);
        }
        
        // Likelihood
        pulled_left ~ binomial(1, p);
    }
"""

posteriori = stan.build(model, data=data_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

samples_chimpanzees = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples,
    observed_data=['pulled_left', 'actor', 'treatment']
)

az.summary(samples_chimpanzees, var_names=['alpha', 'beta'], hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	-0.461	0.340	-1.003	0.072	0.008	0.006	1693.0	2221.0	1.0
alpha[1]	3.899	0.745	2.798	5.136	0.013	0.009	3877.0	2485.0	1.0
alpha[2]	-0.759	0.342	-1.265	-0.181	0.008	0.006	1654.0	2520.0	1.0
alpha[3]	-0.757	0.337	-1.269	-0.205	0.008	0.006	1665.0	2450.0	1.0
alpha[4]	-0.457	0.328	-0.944	0.100	0.008	0.006	1527.0	2448.0	1.0
alpha[5]	0.460	0.336	-0.091	0.978	0.008	0.006	1758.0	2497.0	1.0
alpha[6]	1.948	0.423	1.258	2.606	0.009	0.006	2220.0	2804.0	1.0
beta[0]	-0.028	0.290	-0.494	0.424	0.008	0.005	1494.0	2154.0	1.0
beta[1]	0.489	0.286	0.039	0.953	0.007	0.005	1501.0	2514.0	1.0
beta[2]	-0.374	0.286	-0.813	0.088	0.008	0.005	1422.0	2233.0	1.0
beta[3]	0.380	0.286	-0.063	0.839	0.008	0.005	1409.0	2394.0	1.0

R Code 11.12¶

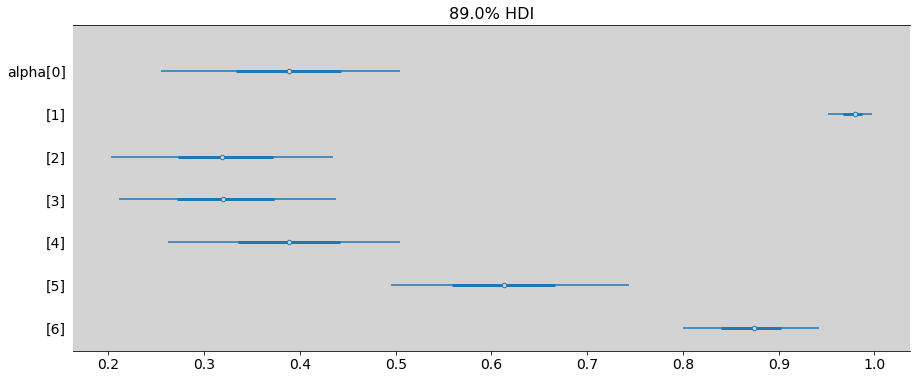
ax = az.plot_forest(samples_chimpanzees, 
                    combined=True,  # Joint all chains 
                    kind="forestplot", # or ridgeplot to plot densities
                    var_names=['alpha'], 
                    transform=inv_logit,
                    hdi_prob=0.89,
                    figsize=(15, 6))

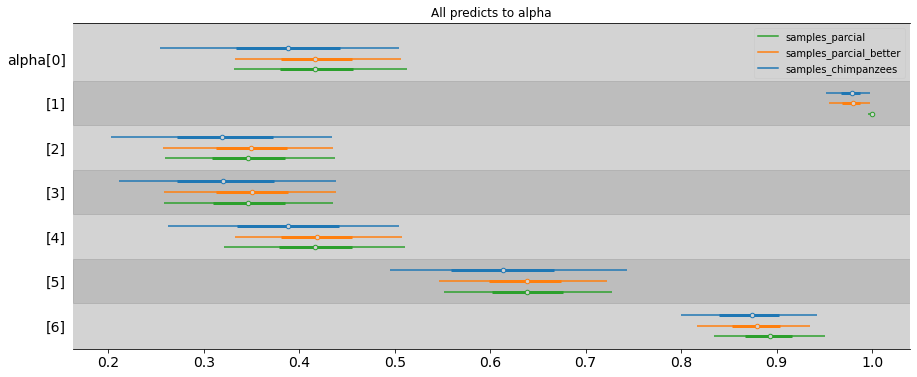
ax = az.plot_forest([samples_chimpanzees, samples_parcial_better, samples_partial], 
                    combined=True,  # Joint all chains 
                    kind="forestplot", # or ridgeplot to plot densities,
                    model_names=['samples_chimpanzees', 'samples_parcial_better', 'samples_parcial'],
                    var_names=['alpha'], 
                    transform=inv_logit,
                    hdi_prob=0.89,
                    figsize=(15, 6))

plt.title('All predicts to alpha')

plt.show()

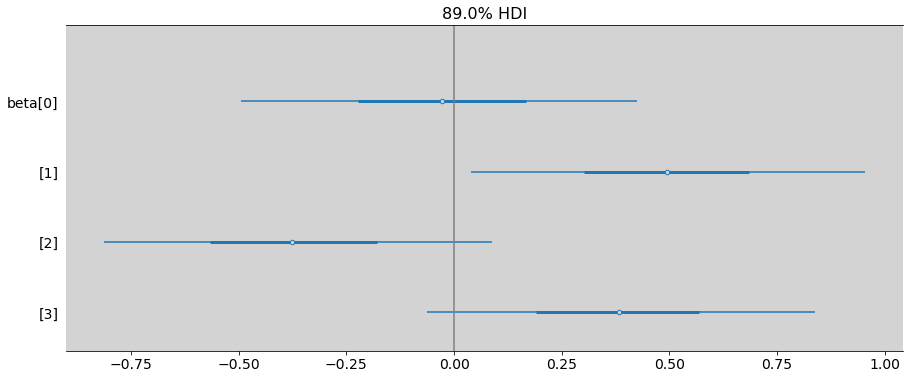
R Code 11.13¶

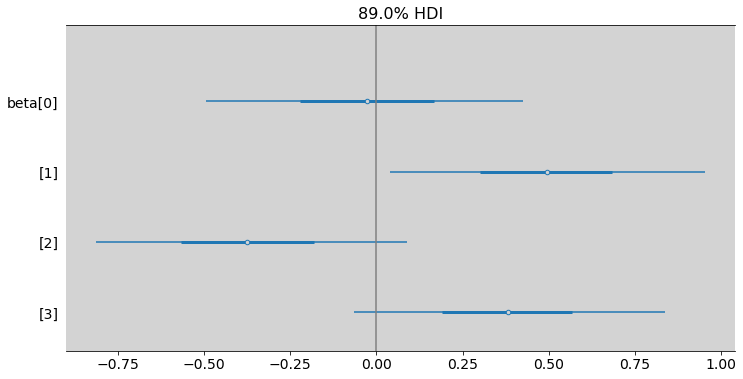
ax = az.plot_forest(samples_chimpanzees, 
                    combined=True,  # Joint all chains 
                    kind="forestplot", # or ridgeplot to plot densities
                    var_names=['beta'], 
                    # transform=inv_logit,
                    hdi_prob=0.89,
                    figsize=(15, 6))
plt.axvline(x=0, c='gray')
plt.show()

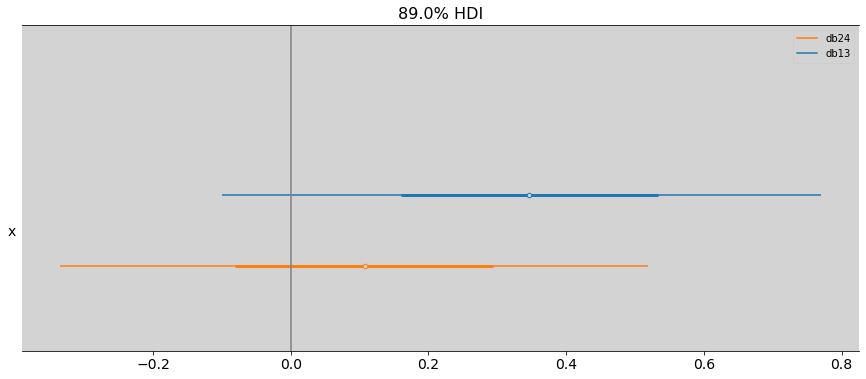
R Code 8.14¶

beta_0 = samples_chimpanzees.posterior.beta.sel(beta_dim_0=0)
beta_1 = samples_chimpanzees.posterior.beta.sel(beta_dim_0=1)
beta_2 = samples_chimpanzees.posterior.beta.sel(beta_dim_0=2)
beta_3 = samples_chimpanzees.posterior.beta.sel(beta_dim_0=3)

diff_beta_0_2 = az.extract(beta_0 - beta_2)
diff_beta_1_3 = az.extract(beta_1 - beta_3)

az.plot_forest(
    [diff_beta_0_2.beta.values, diff_beta_1_3.beta.values],
    combined=True,  # Joint all chains 
    kind="forestplot", # or ridgeplot to plot densities
    # transform=inv_logit,
    model_names=['db13', 'db24'],
    hdi_prob=0.89,
    figsize=(15, 6)
)

plt.axvline(x=0, c='gray')

plt.show()

ax = az.plot_forest(samples_chimpanzees, 
                    combined=True,  # Joint all chains 
                    kind="forestplot", # or ridgeplot to plot densities
                    var_names=['beta'], 
                    # transform=inv_logit,
                    hdi_prob=0.89,
                    figsize=(12, 6))

plt.axvline(x=0, c='gray')
plt.show()

R Code 11.15¶

pl = df.groupby(['actor', 'treatment'])[['actor', 'treatment', 'pulled_left']].mean(['pulled_left'])

pl.loc[pl.actor == 1]

		actor	treatment	pulled_left
actor	treatment
1	1	1.0	1.0	0.333333
	2	1.0	2.0	0.500000
	3	1.0	3.0	0.277778
	4	1.0	4.0	0.555556

R Code 11.16 and R Code 11.17¶

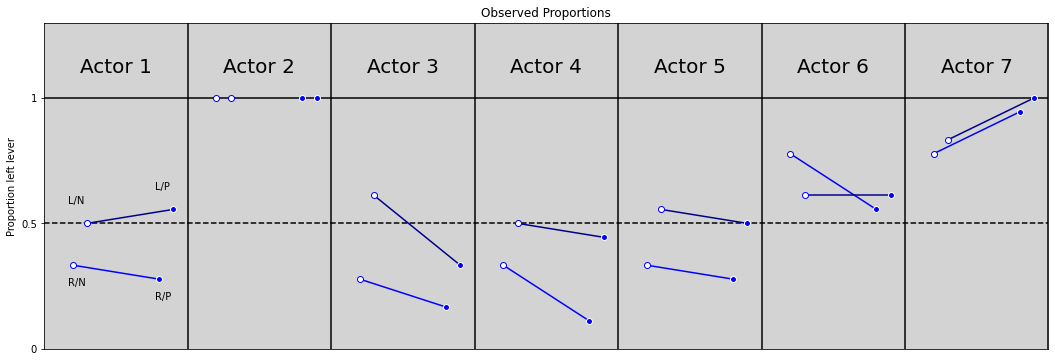
# R Code 11.16

plt.figure(figsize=(18, 6))

plt.ylim(0, 1.3)
plt.xlim(0, 7)
plt.axhline(y=1, ls='-', c='black')
plt.axhline(y=0.5, ls='--', c='black')


for i in range(7):
    plt.axvline(x=i+1, c='black')
    plt.text(x=i + 0.25, y=1.1, s=f'Actor {i + 1}', size=20)
    
    RN, LN, RP, LP = pl.loc[pl.actor == i + 1, 'pulled_left'].values

    if not i == 1:
        plt.plot([0.2 + i, 0.8 + i], [RN, RP], color='blue')
    plt.plot(0.2 + i, RN, 'o', markerfacecolor='white', color='blue')
    plt.plot(0.8 + i, RP, 'o', markerfacecolor='blue', color='white')
    
    if not i == 1:
        plt.plot([0.3 + i, 0.9 + i], [LN, LP], color='darkblue')
    plt.plot(0.3 + i, LN, 'o', markerfacecolor='white', color='blue')
    plt.plot(0.9 + i, LP, 'o', markerfacecolor='blue', color='white')
    
    # Labels for only first points
    if i == 0:
        plt.text(x=0.17, y=RN - 0.08, s='R/N')
        plt.text(x=0.77, y=RP - 0.08, s='R/P')
        plt.text(x=0.17, y=LN + 0.08, s='L/N')
        plt.text(x=0.77, y=LP + 0.08, s='L/P')
    
plt.title('Observed Proportions')
plt.ylabel('Proportion left lever')
plt.yticks([0, 0.5, 1], [0, 0.5, 1])
plt.xticks([])

plt.show()


# R Code 11.17
# ============

plt.figure(figsize=(18, 6))

plt.ylim(0, 1.3)
plt.xlim(0, 7)
plt.axhline(y=1, ls='-', c='black')
plt.axhline(y=0.5, ls='--', c='black')


for i in range(7):
    plt.axvline(x=i+1, c='black')
    plt.text(x=i + 0.25, y=1.1, s=f'Actor {i + 1}', size=20)
    
    alpha_chimp = az.extract(samples_chimpanzees.posterior.alpha.sel(alpha_dim_0=i)).alpha.values
    
    RN = inv_logit(alpha_chimp + az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=0)).beta.values)
    LN = inv_logit(alpha_chimp + az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=1)).beta.values)
    RP = inv_logit(alpha_chimp + az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=2)).beta.values)
    LP = inv_logit(alpha_chimp + az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=3)).beta.values)
    
    # To R/N and R/P
    # ===============
    if not i == 1:
        plt.plot([0.2 + i, 0.8 + i], [RN.mean(), RP.mean()], color='black')
    
    # Plot hdi compatibility interval
    RN_hdi_min, RN_hdi_max = az.hdi(RN, hdi_prob=0.89)
    RP_hdi_min, RP_hdi_max = az.hdi(RP, hdi_prob=0.89)
    plt.plot([0.2 + i, 0.2 + i], [RN_hdi_min, RN_hdi_max], c='black')
    plt.plot([0.8 + i, 0.8 + i], [RP_hdi_min, RP_hdi_max], c='black')
    
    # Plot points
    plt.plot(0.2 + i, RN.mean(), 'o', markerfacecolor='white', color='black')
    plt.plot(0.8 + i, RP.mean(), 'o', markerfacecolor='black', color='white')
    
    # To L/N and L/P
    # ===============
    if not i == 1:
        plt.plot([0.3 + i, 0.9 + i], [LN.mean(), LP.mean()], color='black', linewidth=3)

    # Plot hdi compatibility interval
    LN_hdi_min, LN_hdi_max = az.hdi(LN, hdi_prob=0.89)
    LP_hdi_min, LP_hdi_max = az.hdi(LP, hdi_prob=0.89)
    plt.plot([0.3 + i, 0.3 + i], [LN_hdi_min, LN_hdi_max], c='black')
    plt.plot([0.9 + i, 0.9 + i], [LP_hdi_min, LP_hdi_max], c='black')

    plt.plot(0.3 + i, LN.mean(), 'o', markerfacecolor='white', color='black')
    plt.plot(0.9 + i, LP.mean(), 'o', markerfacecolor='black', color='white')
    
    # Labels for only first points
    if i == 0:
        plt.text(x=0.08, y=RN.mean() - 0.08, s='R/N')
        plt.text(x=0.68, y=RP.mean() - 0.08, s='R/P')
        plt.text(x=0.17, y=LN.mean() + 0.08, s='L/N')
        plt.text(x=0.77, y=LP.mean() + 0.08, s='L/P')
    
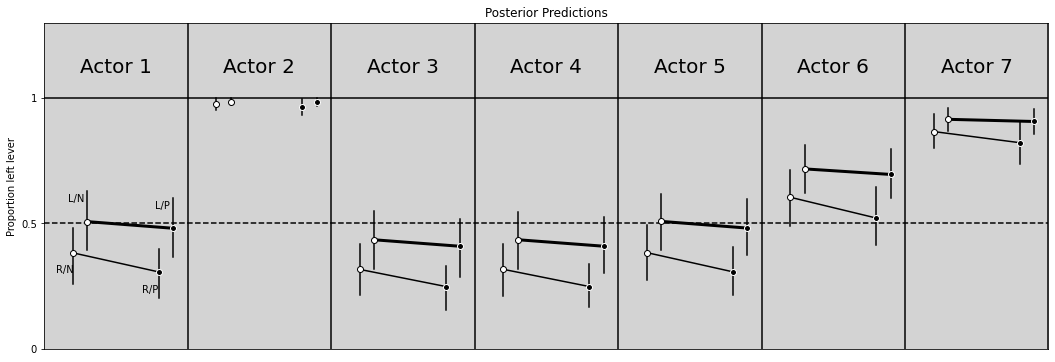
plt.title('Posterior Predictions')
plt.ylabel('Proportion left lever')
plt.yticks([0, 0.5, 1], [0, 0.5, 1])
plt.xticks([])

plt.show()

R Code 11.18¶

df['side'] = df.prosoc_left + 1  # Right 1, Left 2  - Because R start index in 1
df['cond'] = df.condition + 1  # no partner 1, partner 2 - Because R start index in 1

R Code 11.19¶

# Creating data list 2 to model
data_list2 = df[['pulled_left', 'actor', 'side', 'cond']].to_dict('list')
data_list2['N'] = len(df)
data_list2['qty_actors'] = len(df.actor.unique())
data_list2['qty_side'] = len(df.side.unique())
data_list2['qty_cond'] = len(df.cond.unique())

data_list2.keys()

dict_keys(['pulled_left', 'actor', 'side', 'cond', 'N', 'qty_actors', 'qty_side', 'qty_cond'])

model2 = """
    data {
        int N;
        int qty_actors;
        int qty_side;
        int qty_cond;
        
        int pulled_left[N];
        int actor[N];
        int side[N];
        int cond[N];
    }
    
    parameters {
        vector[qty_actors] alpha;
        vector[qty_side] bs;
        vector[qty_cond] bc;
    }
    
    model {
        vector[N] p;
        
        // Prioris
        alpha ~ normal(0, 1.5);
        bs ~ normal(0, 0.5);
        bc ~ normal(0, 0.5);
        
        for (i in 1:N){
            p[i] = alpha[ actor[i] ] + bs[ side[i] ] + bc[ cond[i] ];
            p[i] = inv_logit(p[i]);
        }
        
        // Likelihood
        pulled_left ~ binomial(1, p);
    }
"""

posteriori2 = stan.build(model2, data=data_list2)
samples2 = posteriori2.sample(num_chains=4, num_samples=1000)

samples_chimpanzees_2 = az.from_pystan(
    posterior_model=posteriori2,
    posterior=samples2,
    observed_data=['pulled_left', 'actor', 'side', 'cond']
)

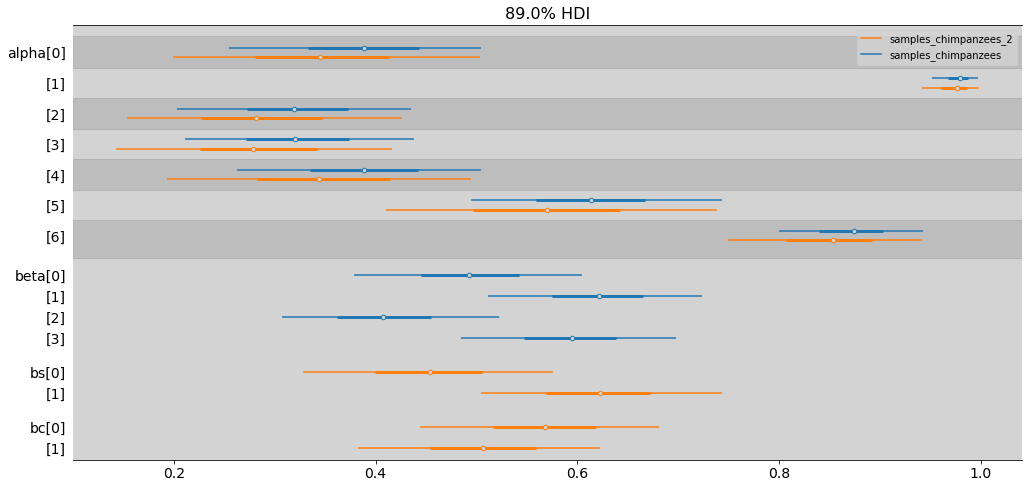
ax = az.plot_forest([samples_chimpanzees, samples_chimpanzees_2],
                    combined=True,  # Joint all chains 
                    kind="forestplot", # or ridgeplot to plot densities
                    var_names=['alpha', 'beta', 'bs', 'bc'], 
                    model_names=['samples_chimpanzees', 'samples_chimpanzees_2'],
                    transform=inv_logit,
                    hdi_prob=0.89,
                    figsize=(17, 8))
plt.show()

R Code 11.21¶

To viewing data from rethinking packages

R Code 11.22¶

Comparing two models

R Code 11.23¶

beta_4 = az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=3)).beta.values
beta_2 = az.extract(samples_chimpanzees.posterior.beta.sel(beta_dim_0=1)).beta.values

np.mean( np.exp(beta_4 - beta_2) )

0.9304928624024834

R Code 11.24¶

d = pd.read_csv('./data/chimpanzees.csv', sep=';')
d['treatment'] = 1 + d['prosoc_left'] + 2 * d['condition']
d['side'] = d['prosoc_left'] + 1  # right 1, left 2
d['cond'] = d['condition'] + 1  # no partner 1, partner 2

d_aggregate = d.groupby(['treatment', 'actor', 'side', 'cond'])[['pulled_left']].sum('pulled_left').copy()
d_aggregate.rename(columns={'pulled_left': 'left_pulls'}, inplace=True)  # Rename columns
d_aggregate.reset_index(inplace=True)
d_aggregate.head(8)

	treatment	actor	side	cond	left_pulls
0	1	1	1	1	6
1	1	2	1	1	18
2	1	3	1	1	5
3	1	4	1	1	6
4	1	5	1	1	6
5	1	6	1	1	14
6	1	7	1	1	14
7	2	1	2	1	9

len(d_aggregate)

R Code 11.25¶

dat = d_aggregate[['left_pulls', 'treatment', 'actor', 'side', 'cond']].to_dict('list')
dat['N'] = len(d_aggregate)
dat['qty_actors'] = len(d_aggregate.actor.unique())
dat['qty_treatments'] = len(d_aggregate.treatment.unique())

dat.keys()

dict_keys(['left_pulls', 'treatment', 'actor', 'side', 'cond', 'N', 'qty_actors', 'qty_treatments'])

model = """
    data {
        int N;
        int qty_actors;
        int qty_treatments;
        
        int left_pulls[N];
        int actor[N];
        int treatment[N];
    }
    
    parameters {
        vector[qty_actors] alpha;
        vector[qty_treatments] beta;
    }
    
    model {
        vector[N] p;
        
        alpha ~ normal(0, 1.5);
        beta ~ normal(0, 0.5);
        
        for (i in 1:N){
            p[i] = alpha[ actor[i] ] + beta[ treatment[i] ];
            p[i] = inv_logit(p[i]);
        }
    
        left_pulls ~ binomial(18, p);
    }
"""

posteriori = stan.build(model, data=dat)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_chimp_bin = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples,
    observed_data=['left_pulls', 'treatment', 'actor'],
)

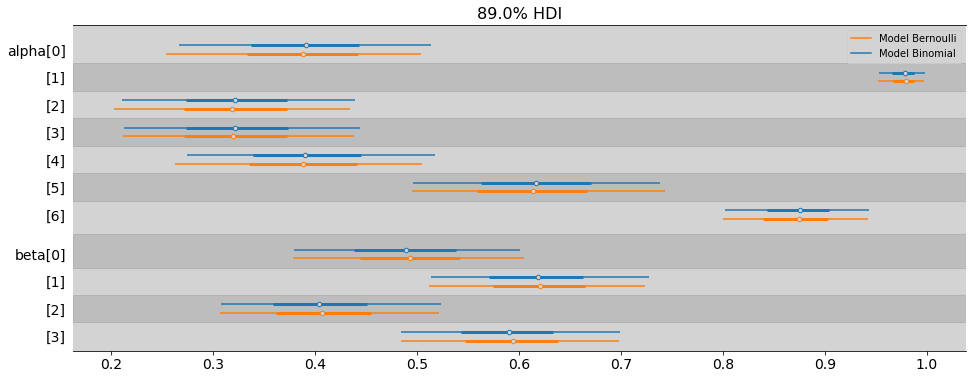
az.plot_forest(
    [model_chimp_bin, samples_chimpanzees],
    var_names=['alpha', 'beta'], 
    model_names=['Model Binomial', 'Model Bernoulli'],
    combined=True, 
    transform=inv_logit, 
    figsize=(16, 6),
    hdi_prob=0.89,
)

plt.show()

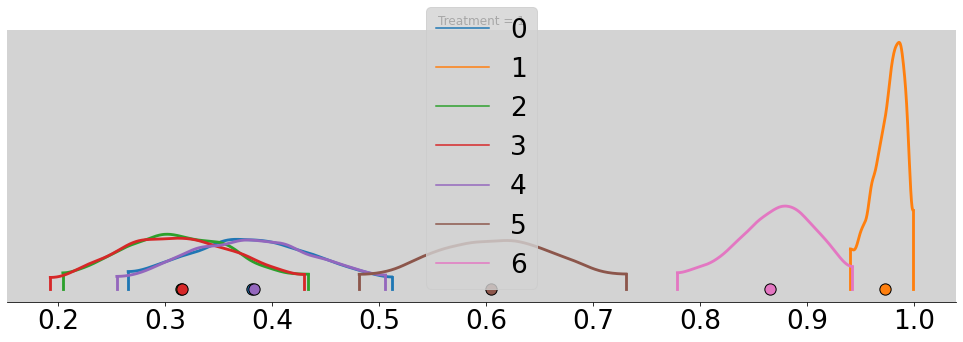
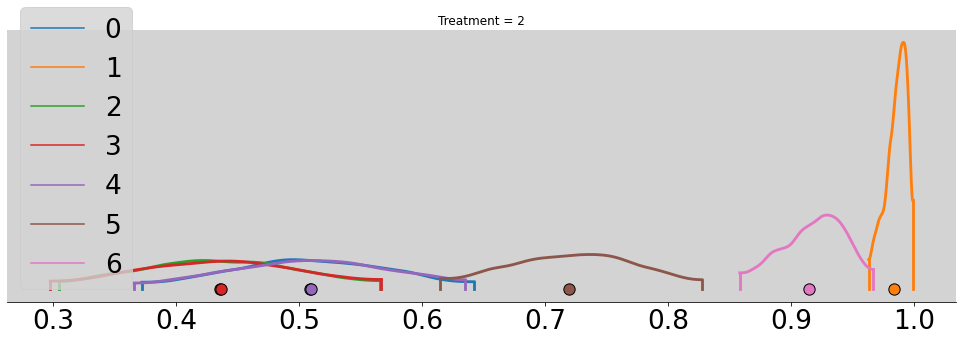
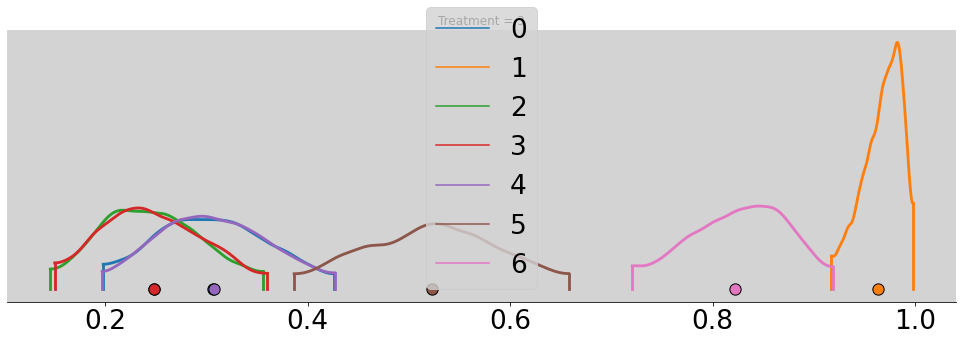
for t in range(4):
    p_chimp_bin = []
    for i in range(7):
        alpha_chimp_bin = model_chimp_bin.posterior.alpha.sel(alpha_dim_0=i).values.flatten()
        beta_chimp_bin = model_chimp_bin.posterior.beta.sel(beta_dim_0=t).values.flatten()

        p_chimp_bin.append(inv_logit(alpha_chimp_bin + beta_chimp_bin))

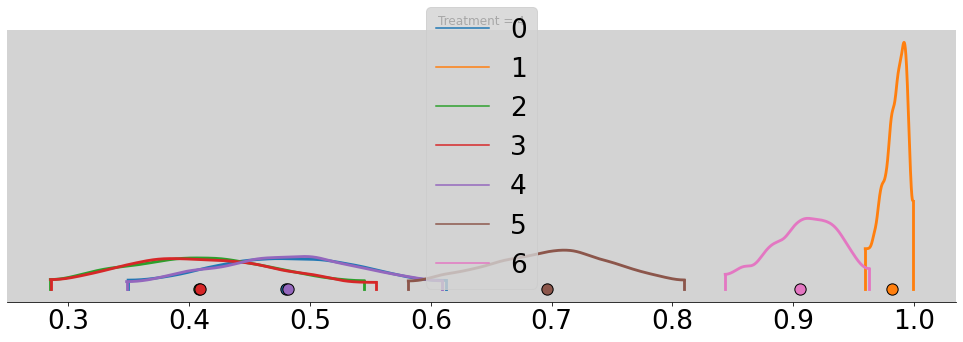
    az.plot_density(p_chimp_bin, figsize=(17, 5))
    plt.title(f'Treatment = {t + 1}')

plt.show()

R Code 11.26¶

models_to_compare = {'model_chimp_bin': model_chimp_bin, 'samples_chimpanzees': samples_chimpanzees}

# az.compare(models_to_compare)  # or use 'elpd_waic' to WAIC

# XXX: Need to make posteriori in model to read in arviz

R Code 11.27¶

# Deviance of aggregated 6-in-9
agg = -2 * np.log(stats.binom.pmf(k=6, n=9, p=0.2))
print(agg)

# Deviance of dis-aggregagted
k = [1, 1, 1, 1, 1, 1, 0, 0, 0]

not_agg = -2 * np.sum(np.log(stats.bernoulli.pmf(k=k, p=0.2)))
print(not_agg)

11.790482659407832
20.652116257094463

My Tests¶

N = 100
p = np.random.rand()

y = np.random.binomial(1, p, N)

model = """
    data{
        int N;
        int y[N];
    }
    
    parameters {
        real alpha;
    }
    
    model {
        vector[N] p;
        
        // Priori
        alpha ~ normal(0.5, 1);
    
        for (i in 1:N){
                p[i] = inv_logit(alpha);
        }
    
        // Likelihood
        y ~ binomial(1, p);
    }
"""

data = {
    'N':N,
    'y': y,
}

posteriori = stan.build(model, data=data)
samples_test = posteriori.sample(num_chains=4, num_samples=1000)

samples_test_az = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples_test,
    observed_data=['y']
)

az.plot_density(
    samples_test_az, var_names=['alpha'], 
    transform=inv_logit)

az.plot_density(
    samples_test_az, var_names=['alpha'])

az.plot_density(inv_logit(np.random.normal(0.5, 0.5, 1000)))  # Priori

plt.show()

print(p, np.mean(inv_logit(samples_test_az.posterior.alpha.values)))

0.6395421321747394 0.5988337119128063

az.plot_density(inv_logit(samples_test_az.posterior.alpha.values) - p)
plt.show()

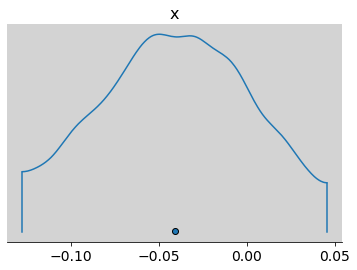
# Binomial

N = 100
p = np.random.rand()

y = np.random.binomial(5, p, N)

model = """
    data{
        int N;
        int y[N];
    }
    
    parameters {
        real alpha;
    }
    
    model {
        vector[N] p;
        
        // Priori
        alpha ~ normal(0.5, 1);
    
        for (i in 1:N){
                p[i] = inv_logit(alpha);
        }
    
        // Likelihood
        y ~ binomial(5, p);
    }
"""

data = {
    'N':N,
    'y': y,
}

posteriori = stan.build(model, data=data)
samples_test = posteriori.sample(num_chains=4, num_samples=1000)

samples_test_az = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples_test,
    observed_data=['y']
)

az.plot_density(
    samples_test_az, var_names=['alpha'], 
    transform=inv_logit)

az.plot_density(
    samples_test_az, var_names=['alpha'])

plt.show()

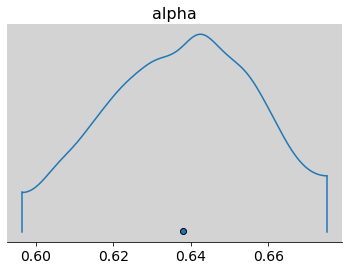
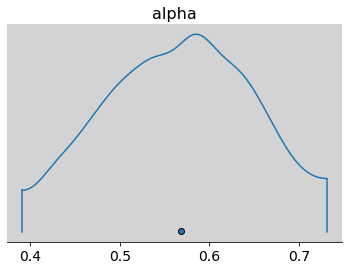
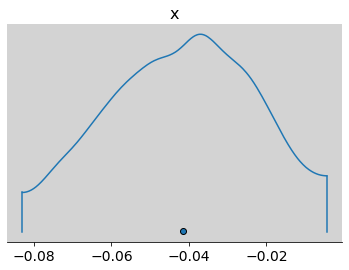
print(p, np.mean(inv_logit(samples_test_az.posterior.alpha.values)))

0.679474227457576 0.6379739000951222

az.plot_density(inv_logit(samples_test_az.posterior.alpha.values) - p)
plt.show()

R Code 11.28¶

df = pd.read_csv('./data/UCBadmit.csv', sep=';')
df

	dept	applicant.gender	admit	reject	applications
1	A	male	512	313	825
2	A	female	89	19	108
3	B	male	353	207	560
4	B	female	17	8	25
5	C	male	120	205	325
6	C	female	202	391	593
7	D	male	138	279	417
8	D	female	131	244	375
9	E	male	53	138	191
10	E	female	94	299	393
11	F	male	22	351	373
12	F	female	24	317	341

total_male_applic = df[df['applicant.gender']  == 'male']['applications'].sum()
total_male_admit = df[df['applicant.gender']  == 'male']['admit'].sum()
print('Percentual total male =', int(100*(total_male_admit / total_male_applic)), '%')

total_female_applic = df[df['applicant.gender']  == 'female']['applications'].sum()
total_female_admit = df[df['applicant.gender']  == 'female']['admit'].sum()
print('Percentual total female =', int(100*(total_female_admit / total_female_applic)), '%')

Percentual total male = 44 %
Percentual total female = 30 %

R Code 11.29¶

\[ A_i \sim Binomial(N_i, p_i) \]

\[ logit(p_i) = \alpha_{GID[i]} \]

\[ \alpha_j \sim Normal(0, 1.5) \]

df['gid'] = np.where(df['applicant.gender'] == 'male', 1, 2)

dat_list = df[['admit', 'applications', 'gid']].to_dict('list')
dat_list['N'] = len(df)
dat_list['qty_genders'] = len(df.gid.unique())
dat_list

{'admit': [512, 89, 353, 17, 120, 202, 138, 131, 53, 94, 22, 24],
 'applications': [825, 108, 560, 25, 325, 593, 417, 375, 191, 393, 373, 341],
 'gid': [1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2],
 'N': 12,
 'qty_genders': 2}

for dept_i in df.dept.unique():
    
    print(f'DEPARTMENT ---> {dept_i}')
        
    for gend_i in ['male', 'female']:
    
        applications = df[(df['dept'] == dept_i) & (df['applicant.gender'] == gend_i)]['applications']
        admit = df[(df['dept'] == dept_i) & (df['applicant.gender'] == gend_i)]['admit']
        perc_admit = admit.values / applications.values

        print(f'The dept {dept_i} has {int(100 * perc_admit[0])}% acceptions rate for {gend_i}')
        
    print('\n')

DEPARTMENT ---> A
The dept A has 62% acceptions rate for male
The dept A has 82% acceptions rate for female


DEPARTMENT ---> B
The dept B has 63% acceptions rate for male
The dept B has 68% acceptions rate for female


DEPARTMENT ---> C
The dept C has 36% acceptions rate for male
The dept C has 34% acceptions rate for female


DEPARTMENT ---> D
The dept D has 33% acceptions rate for male
The dept D has 34% acceptions rate for female


DEPARTMENT ---> E
The dept E has 27% acceptions rate for male
The dept E has 23% acceptions rate for female


DEPARTMENT ---> F
The dept F has 5% acceptions rate for male
The dept F has 7% acceptions rate for female

model = """
    data {
        int N;
        int qty_genders;
        
        int admit[N];
        int applications[N];
        int gid[N];
    }
    
    parameters {
        vector[qty_genders] alpha;
    }
    
    model {
        vector[N] p;
        
        alpha ~ normal(0, 1.5);
        
        for (i in 1:N){
            p[i] = alpha[ gid[i] ];
            p[i] = inv_logit(p[i]);
        }
        
        admit ~ binomial(applications, p);
    }
"""

posteriori = stan.build(model, data=dat_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

app_gender = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples,
    observed_data=list(dat_list.keys()),
    dims={
        'alpha': ['gender'],
    }
)

az.summary(app_gender)  # In scale inv-logit

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	-0.22	0.039	-0.287	-0.143	0.001	0.000	3893.0	2712.0	1.0
alpha[1]	-0.83	0.050	-0.921	-0.733	0.001	0.001	4089.0	2650.0	1.0

az.plot_forest(app_gender, var_names=['alpha'], combined=True, figsize=(15,5), transform=inv_logit)
plt.show()

R Code 11.30¶

alpha_1 = app_gender.posterior.alpha.sel(gender=0)
alpha_2 = app_gender.posterior.alpha.sel(gender=1)

diff_a = alpha_1 - alpha_2
diff_p = inv_logit(alpha_1) - inv_logit(alpha_2)

az.summary(diff_a)  # Shark

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	0.61	0.065	0.49	0.734	0.001	0.001	4040.0	2912.0	1.0

az.summary(diff_p)  # Deer

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	0.141	0.015	0.114	0.169	0.0	0.0	4030.0	2886.0	1.0

R Code 11.31¶

plt.figure(figsize=(18, 6))

plt.ylim(0, 1.3)
plt.xlim(0, 5.8)
plt.axhline(y=1, ls='-', c='black')

depts = df.dept.unique()

for i in range(6):
    plt.axvline(x=i+1, c='black')
    
    dept = depts[i]

    plt.text(x=i + 0.25, y=1.1, s=f'Dept {dept}', size=20)

    perc_male, perc_female = df.loc[df['dept'] == dept, 'admit'] / df.loc[df['dept'] == dept, 'applications']

    plt.plot([0.2 + i, 0.7 + i], [perc_male, perc_female], color='blue')  # Line
    plt.plot(0.2 + i, perc_male, 'o', markerfacecolor='white', color='blue')  # point male
    plt.plot(0.7 + i, perc_female, 'o', markerfacecolor='blue', color='white')  # point female
    
    plt.text(x=0.5 + i, y=max(perc_male, perc_female) + 0.05, s=dept)
    
plt.title('Posteriori Validation Check')
plt.ylabel('Admit')
plt.xlabel('Case')
plt.yticks([0, 0.2, 0.4, 0.6, 0.8, 1.0], [0, 0.2, 0.4, 0.6, 0.8, 1])
plt.xticks(np.arange(0, 5.9, 0.5) + 0.2, np.arange(1, 12.1, 1, dtype=int))

plt.show()

# Need put points with open points from samples

R Code 11.32¶

We want ask:

- What is the average difference in probability of admission between women and man within departments?

\[ A_i \sim Binomial(N_i, p_i) \]

\[ logit(p_i) = \alpha_{GID[i]} + \delta_{DEPT[i]} \]

\[ \alpha_j \sim Normal(0, 1.5) \]

\[ \delta_k \sim Normal(0, 1.5) \]

df['gid'] = np.where(df['applicant.gender'] == 'male', 1, 2)

df['dept_idx'] = [ord(dept_i) - 64 for dept_i in df['dept']]  # ord('A') = 65

dat_list = df[['admit', 'applications', 'gid', 'dept_idx']].to_dict('list')
dat_list['N'] = len(df)
dat_list['qty_genders'] = len(df.gid.unique())
dat_list['qty_dept'] = len(df.dept_idx.unique())

dat_list

{'admit': [512, 89, 353, 17, 120, 202, 138, 131, 53, 94, 22, 24],
 'applications': [825, 108, 560, 25, 325, 593, 417, 375, 191, 393, 373, 341],
 'gid': [1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2],
 'dept_idx': [1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6],
 'N': 12,
 'qty_genders': 2,
 'qty_dept': 6}

model = """
    data {
        int N;
        int qty_genders;
        int qty_dept;
        
        array[N] int admit;
        array[N] int applications;
        array[N] int gid;
        array[N] int dept_idx;
    }
    
    parameters {
        vector[qty_genders] alpha;
        vector[ qty_dept ] delta;
    }
    
    model {
        vector[N] p;
        
        alpha ~ normal(0, 1.5);
        delta ~ normal(0, 1.5);
        
        for (i in 1:N){
            p[i] = alpha[ gid[i] ] + delta[ dept_idx[i] ];  # O Delta calcula a taxa média de admissão para o departamento i
            p[i] = inv_logit(p[i]);
        }
        
        admit ~ binomial(applications, p);
    }
"""

posteriori = stan.build(model, data=dat_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

applic_gender_2 = az.from_pystan(
    posterior_model=posteriori,
    posterior=samples,
    observed_data=list(dat_list.keys()),
    dims = {
        'alpha': ['gender'],
        'delta': ['department'],
    }
)

az.summary(applic_gender_2)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	-0.602	0.521	-1.479	0.429	0.03	0.021	309.0	552.0	1.0
alpha[1]	-0.506	0.523	-1.420	0.482	0.03	0.021	307.0	582.0	1.0
delta[0]	1.183	0.525	0.229	2.153	0.03	0.021	311.0	597.0	1.0
delta[1]	1.138	0.527	0.141	2.098	0.03	0.021	313.0	618.0	1.0
delta[2]	-0.076	0.524	-1.036	0.880	0.03	0.021	309.0	579.0	1.0
delta[3]	-0.108	0.525	-1.055	0.858	0.03	0.021	308.0	575.0	1.0
delta[4]	-0.552	0.528	-1.580	0.371	0.03	0.021	307.0	621.0	1.0
delta[5]	-2.111	0.538	-3.131	-1.141	0.03	0.021	323.0	623.0	1.0

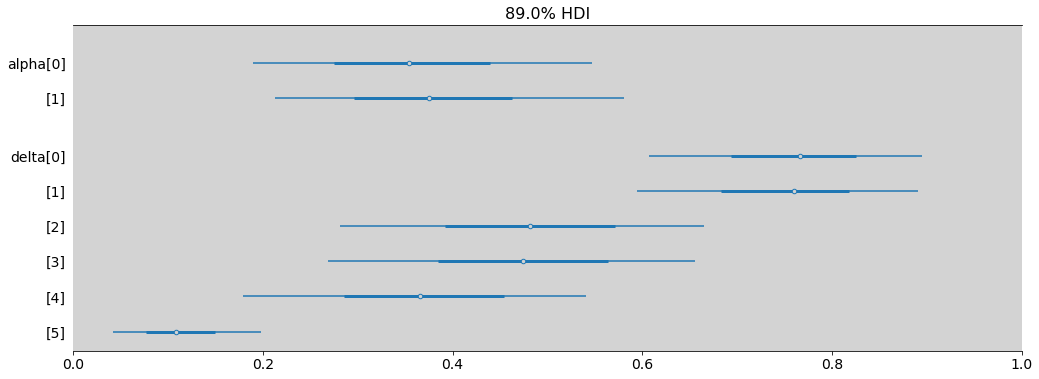
az.plot_forest(
    applic_gender_2,
    var_names=['alpha', 'delta'],
    combined=True,
    transform=inv_logit,
    figsize=(17, 6),
    hdi_prob=0.89,
)

plt.xlim((0, 1))
plt.show()

R Code 11.33¶

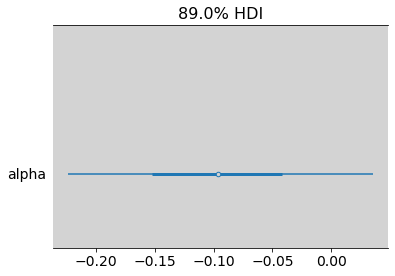
alpha_male = applic_gender_2.posterior.alpha.sel(gender=0)
alpha_female = applic_gender_2.posterior.alpha.sel(gender=1)

az.summary(alpha_male - alpha_female, hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	-0.096	0.081	-0.223	0.035	0.001	0.001	4495.0	3760.0	1.0

az.plot_forest((alpha_male - alpha_female), hdi_prob=0.89, combined=True)
plt.show()

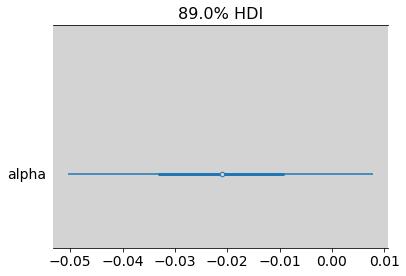
az.summary(inv_logit(alpha_male) - inv_logit(alpha_female), hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	-0.021	0.018	-0.05	0.008	0.0	0.0	3438.0	3591.0	1.0

az.plot_forest((inv_logit(alpha_male) - inv_logit(alpha_female)), hdi_prob=0.89, combined=True)
plt.show()

pg = {}
pg['male'] = {}
pg['female'] = {}

dept_i = 'A'

for dept_i in df['dept'].unique():

    total = df[df['dept'] == dept_i]['applications'].sum()
    total_male = df[(df['dept'] == dept_i) & (df['applicant.gender'] == 'male')]['applications'].sum()
    total_female = df[(df['dept'] == dept_i) & (df['applicant.gender'] == 'female')]['applications'].sum()

    pg['male'][dept_i] = round(total_male / total, 2)
    pg['female'][dept_i] = round(total_female / total, 2)
    
pd.DataFrame.from_dict(pg).T

	A	B	C	D	E	F
male	0.88	0.96	0.35	0.53	0.33	0.52
female	0.12	0.04	0.65	0.47	0.67	0.48

Poisson Regression¶

R Code 11.35¶

N = 10000
p = 1/1000

y = np.random.binomial(N, p, 10000)
print(f'The mean is {np.mean(y)} and variance is {np.var(y)}')

The mean is 10.036 and variance is 10.078504

R Code 11.36¶

df = pd.read_csv('./data/Kline.csv', sep=';')
df

	culture	population	contact	total_tools	mean_TU
0	Malekula	1100	low	13	3.2
1	Tikopia	1500	low	22	4.7
2	Santa Cruz	3600	low	24	4.0
3	Yap	4791	high	43	5.0
4	Lau Fiji	7400	high	33	5.0
5	Trobriand	8000	high	19	4.0
6	Chuuk	9200	high	40	3.8
7	Manus	13000	low	28	6.6
8	Tonga	17500	high	55	5.4
9	Hawaii	275000	low	71	6.6

\[ y_i \sim Poisson(\lambda) \]

The parameter \(\lambda\) is expected value of the outcome y.

The link function for poisson is the \(log\) link.

\[ y_i \sim Poisson(\lambda_i) \]

\[ log(\lambda_i) = \alpha + \beta(x_i - \bar x) \]

R Code 11.37¶

df['log_population'] = np.log(df['population'])  # log population
df['P'] = (df['log_population'] - np.mean(df['log_population'])) / np.std(df['log_population'])  #std log population
df['contact_id'] = [2 if contact_i == 'high' else 1 for contact_i in df['contact'].values ]  # CID 1:low; 2:high
df

	culture	population	contact	total_tools	mean_TU	log_population	P	contact_id
0	Malekula	1100	low	13	3.2	7.003065	-1.361332	1
1	Tikopia	1500	low	22	4.7	7.313220	-1.147433	1
2	Santa Cruz	3600	low	24	4.0	8.188689	-0.543664	1
3	Yap	4791	high	43	5.0	8.474494	-0.346558	2
4	Lau Fiji	7400	high	33	5.0	8.909235	-0.046737	2
5	Trobriand	8000	high	19	4.0	8.987197	0.007029	2
6	Chuuk	9200	high	40	3.8	9.126959	0.103416	2
7	Manus	13000	low	28	6.6	9.472705	0.341861	1
8	Tonga	17500	high	55	5.4	9.769956	0.546861	2
9	Hawaii	275000	low	71	6.6	12.524526	2.446558	1

Model - Poisson Regression¶

\[ T_i \sim Poisson(\lambda_i) \]

\[ log(\lambda_i) = \alpha_{CID[i]} + \beta_{CID[i]} log(P_i) \]

\[ \alpha_j \sim \mbox{to be determined} \]

\[ \beta_j \sim \mbox{to be determined} \]

\[ T_i \sim Poisson(\lambda_i) \]

\[ log(\lambda_i) = \alpha\]

\[ \alpha \sim Normal(0, 10) \]

R Code 11.38¶

plt.figure(figsize=(17, 6))

N = 200
x = np.linspace(0, 100, N)

y = stats.lognorm.pdf(x=x, s=10, loc=0, scale=20)  # See the docs to understanding the parameters

# R Code 11.40
y_new = stats.lognorm.pdf(x=x, s=0.5, loc=3, scale=20)  # See the docs to understanding the parameters

plt.plot(x, y, c='black')
plt.plot(x, y_new, c='blue')

plt.ylabel('Density')
plt.xlabel('Mean Number of Tools')

plt.show()

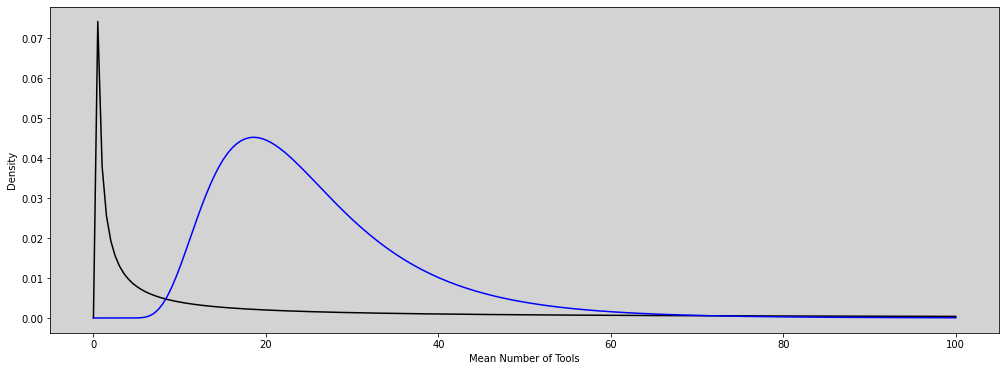
R Code 11.39¶

a = np.random.normal(0, 10, 1000)
lambda_ = np.exp(a)
np.mean(lambda_)

1877154437902.8613

R Code 11.40¶

# Ploted in R Code 11.38

R Code 11.41¶

N = 100
a = np.random.normal(3, 0.5, N)  # prior to alpha
b = np.random.normal(0, 10, N)  # prior to beta

x = np.linspace(-2, 2, 100)

prioris = []

plt.figure(figsize=(17, 6))

for i in range(N):
    plt.plot(x, np.exp(a[i] + b[i] * x), c='blue')
    
plt.xlim(-2, 2)
plt.ylim(0, 100)

plt.title('Poisson Priori \n beta ~ Normal(0, 10)')
plt.xlabel('log population (std)')
plt.ylabel('total odds')
    
plt.show()

R Code 11.42¶

N = 100
a = np.random.normal(3, 0.5, N)  # prior to alpha
b = np.random.normal(0, 0.2, N)  # prior to beta

x = np.linspace(-2, 2, 100)

prioris = []

plt.figure(figsize=(17, 6))
for i in range(N):
    plt.plot(x, np.exp(a[i] + b[i] * x), c='blue')
    
plt.xlim(-2, 2)
plt.ylim(0, 100)

plt.title('Poisson Priori \n beta ~ Normal(0, 0.2)')
plt.xlabel('log population (std)')
plt.ylabel('total odds')

plt.show()

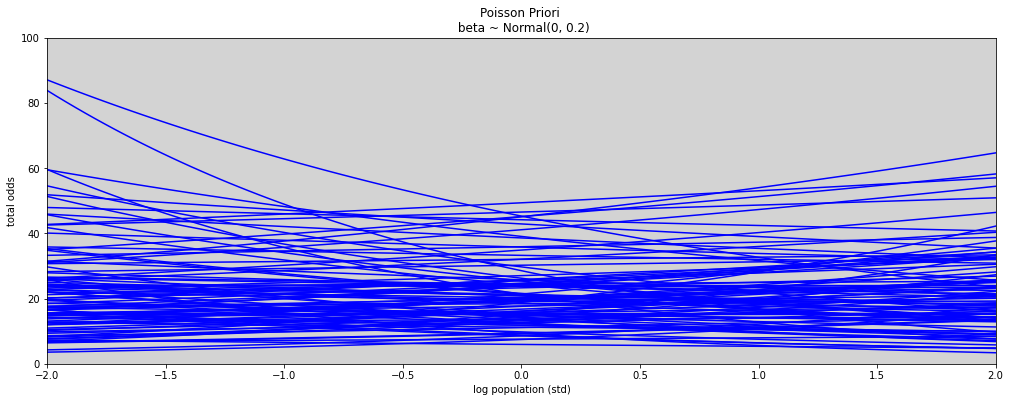
R Code 11.43¶

N = 100
a = np.random.normal(3, 0.5, N)  # prior to alpha
b = np.random.normal(0, 0.2, N)  # prior to beta

x_seq = np.linspace(np.log(100), np.log(200000), 100)  # log(population)

lambda_poisson =  [ np.exp(a[i] + b[i] * x_seq) for i in range(N) ]

plt.figure(figsize=(17,6))

for i in range(N):
    plt.plot(x_seq, lambda_poisson[i], c='blue')

plt.ylim(0, 500)
plt.xlim(min(x_seq) - 0.1, max(x_seq))

plt.title('a ~ Normal(3, 0.5), b ~ Normal(0, 0.2)')
plt.xlabel('log population')
plt.ylabel('total tools')

plt.show()

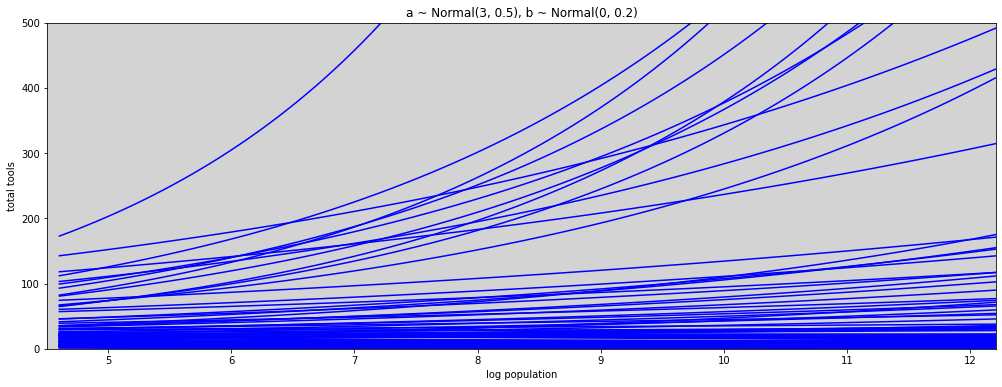
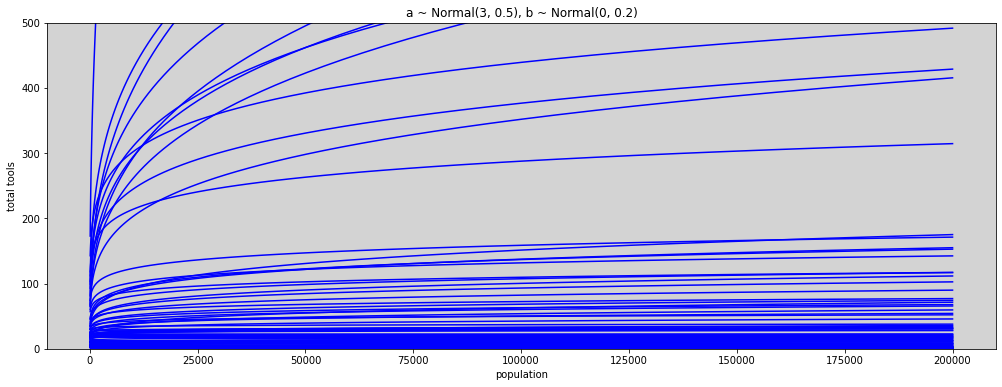
R Code 11.44¶

#N = 100
#a = np.random.normal(3, 0.5, N)  # prior to alpha
#b = np.random.normal(0, 0.2, N)  # prior to beta

x_seq = np.linspace(np.log(100), np.log(200000), 100)  # log(population)

lambda_poisson_ =  [ np.exp(a[i] + b[i] * x_seq) for i in range(N) ]

plt.figure(figsize=(17,6))

for i in range(N):
    plt.plot(np.exp(x_seq), lambda_poisson_[i], c='blue')

plt.ylim(0, 500)
#plt.xlim(min(np.exp(x_seq)), max(np.exp(x_seq)))

plt.title('a ~ Normal(3, 0.5), b ~ Normal(0, 0.2)')
plt.xlabel('population')
plt.ylabel('total tools')

plt.show()

Curiosidade do python¶

x = np.linspace(0, 10, 100)
y = np.exp(2 + 4 * x)

plt.plot(x*2000, y, c='red')
plt.show()

plt.plot(np.exp(x), y, c='red')
plt.show()

plt.plot(x*2000, y, c='red')
plt.show()

R Code 11.45¶

Model:¶

\[ T_i \sim Poisson(\lambda_i) \]

\[ log(\lambda_i) = \alpha_{CID[i]} \]

\[ \alpha_j \sim Normal(3, 0.5) \]

model_11_9 = """
    data {
        int N;
        array[N] int total_tools;
    }
    
    parameters {
        real alpha;
    }
    
    model {
        // Priori
        alpha ~ normal(3, 0.5);
        
        // Likelihood
        total_tools ~ poisson(exp(alpha));
    }
"""

data_list = df[['total_tools']].to_dict('list')
data_list['N'] = len(df)

posteriori = stan.build(model_11_9, data=data_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_11_9_post = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
    observed_data=list(data_list.keys()),
)

az.summary(model_11_9_post, var_names=['alpha'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	3.539	0.053	3.437	3.634	0.001	0.001	1653.0	2031.0	1.0

az.plot_forest(model_11_9_post, var_names=['alpha'], combined=True)
plt.show()

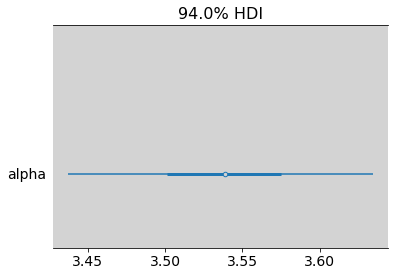
Model:¶

\[ T_i \sim Poisson(\lambda_i) \]

\[ log(\lambda_i) = \alpha_{CID[i]} + \beta_{CID[i]} \times log(P_i) \]

\[ \alpha_j \sim Normal(3, 0.5) \]

\[ \beta_j \sim Normal(0, 0.2) \]

model_11_9_new = """
    data {
        int N;
        int qty_cid;
        array[N] int total_tools;
        array[N] real P;
        array[N] int contact_id;
    }
    
    parameters {
        array[qty_cid] real alpha;
        array[qty_cid] real beta;
    }
    
    model {
        vector[N] lambda;
        
        // Priori
        alpha ~ normal(3, 0.5);
        beta ~ normal(0, 0.2);
        
        // Likelihood
        for(i in 1:N){
                lambda[i] = alpha[ contact_id[i] ] + beta[ contact_id[i] ] * P[i];
                lambda[i] = exp(lambda[i]);
        }
        total_tools ~ poisson(lambda);
    }
"""

data_list = df[['total_tools', 'P', 'contact_id']].to_dict('list')
data_list['N'] = len(df)
data_list['qty_cid'] = len(df.contact_id.unique())

posteriori = stan.build(model_11_9_new, data=data_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_11_9_new_post = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
    observed_data=list(data_list.keys()),
    dims={
        'alpha': ['contact_id'],
        'beta': ['contact_id'],
    }
)

az.summary(model_11_9_new_post)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	3.318	0.085	3.159	3.475	0.002	0.001	3218.0	3262.0	1.0
alpha[1]	3.610	0.072	3.465	3.737	0.001	0.001	3837.0	2567.0	1.0
beta[0]	0.361	0.049	0.265	0.449	0.001	0.001	3990.0	3160.0	1.0
beta[1]	0.189	0.156	-0.123	0.468	0.003	0.002	3815.0	2813.0	1.0

az.plot_forest(model_11_9_new_post, var_names=['alpha', 'beta'], combined=True, figsize=(17, 5))
plt.show()

R Code 11.46¶

# Need to make a generated_quantities to compute compare


dict_to_compare = {
    'model_11_9_post': model_11_9_post,
    'model_11_9_new_post': model_11_9_new_post
}

# az.compare(dict_to_compare)

R Code 11.47¶

N = 100
a_low = model_11_9_new_post.posterior.alpha.sel(contact_id=0).values.flatten()  # CID = 0 (low contact) 
b_low = model_11_9_new_post.posterior.beta.sel(contact_id=0).values.flatten()  # CID = 0 (low contact)

a_high = model_11_9_new_post.posterior.alpha.sel(contact_id=1).values.flatten()  # CID = 1 (high contact) 
b_high = model_11_9_new_post.posterior.beta.sel(contact_id=1).values.flatten()  # CID = 1 (high contact)

x_seq = np.linspace(-1.4, 3, 100)  # log(population)

lambda_poisson_low =  np.array([ np.exp(a_low + b_low * x_seq[i]) for i in range(N)])
hdi_low = np.transpose([ az.hdi(lambda_poisson_low[i]) for i in range(N) ])
            
lambda_poisson_high =  np.array([ np.exp(a_high + b_high * x_seq[i]) for i in range(N)])
hdi_high = np.transpose([ az.hdi(lambda_poisson_high[i]) for i in range(N) ])

plt.figure(figsize=(17,8))

plt.plot(x_seq,lambda_poisson_low.mean(axis=1), c='blue', label='Low', ls='--')  # Low
plt.fill_between(x_seq, hdi_low[0], hdi_low[1], color='blue', alpha=0.1)

plt.plot(x_seq, lambda_poisson_high.mean(axis=1), c='black', label='High')  # High
plt.fill_between(x_seq, hdi_high[0], hdi_high[1], color='black', alpha=0.1)

# Plot the points
plt.scatter(df[df['contact_id'] == 1].P, df[df['contact_id'] == 1].total_tools, label='Low contact', color='blue')
plt.scatter(df[df['contact_id'] == 2].P, df[df['contact_id'] == 2].total_tools, label='High contact', color='black')

plt.title('')
plt.xlabel('log population (std)')
plt.ylabel('total tools')
plt.legend(loc='upper left')


plt.show()

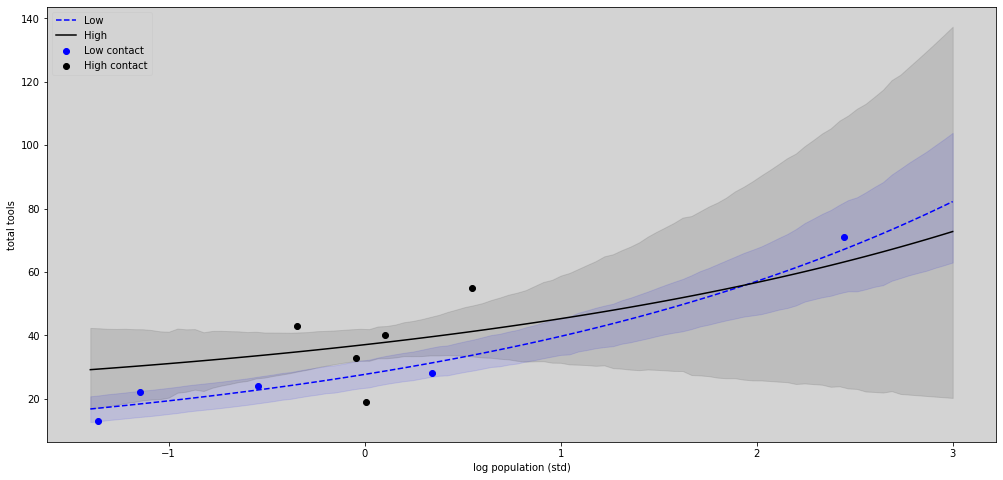
R Code 11.48¶

N = 100
a_low = model_11_9_new_post.posterior.alpha.sel(contact_id=0).values.flatten()  # CID = 0 (low contact) 
b_low = model_11_9_new_post.posterior.beta.sel(contact_id=0).values.flatten()  # CID = 0 (low contact)

a_high = model_11_9_new_post.posterior.alpha.sel(contact_id=1).values.flatten()  # CID = 1 (high contact) 
b_high = model_11_9_new_post.posterior.beta.sel(contact_id=1).values.flatten()  # CID = 1 (high contact)

p_seq = np.linspace(-5, 3, 100)

# 1.53 is sd of log(population)
# 9 is mean of log(population)
pop_seq = np.exp(p_seq * 1.53 + 9)

lambda_poisson_low =  np.array([ np.exp(a_low + b_low * p_seq[i]) for i in range(N)])
hdi_low = np.transpose([ az.hdi(lambda_poisson_low[i]) for i in range(N) ])
            
lambda_poisson_high =  np.array([ np.exp(a_high + b_high * p_seq[i]) for i in range(N)])
hdi_high = np.transpose([ az.hdi(lambda_poisson_high[i]) for i in range(N) ])

plt.figure(figsize=(17,8))

plt.plot(pop_seq,lambda_poisson_low.mean(axis=1), c='blue', label='Low', ls='--')  # Low
plt.fill_between(pop_seq, hdi_low[0], hdi_low[1], color='blue', alpha=0.1)

plt.plot(pop_seq, lambda_poisson_high.mean(axis=1), c='black', label='High')  # High
plt.fill_between(pop_seq, hdi_high[0], hdi_high[1], color='black', alpha=0.1)

# Plot the points
plt.scatter(df[df['contact_id'] == 1].population, df[df['contact_id'] == 1].total_tools, label='Low contact', color='blue')
plt.scatter(df[df['contact_id'] == 2].population, df[df['contact_id'] == 2].total_tools, label='High contact', color='black')

# Limits graphs
plt.xlim(-10000, 300000)
plt.ylim(-3, 90)

plt.title('')
plt.xlabel('population')
plt.ylabel('total tools')
plt.legend(loc='upper left')

plt.show()

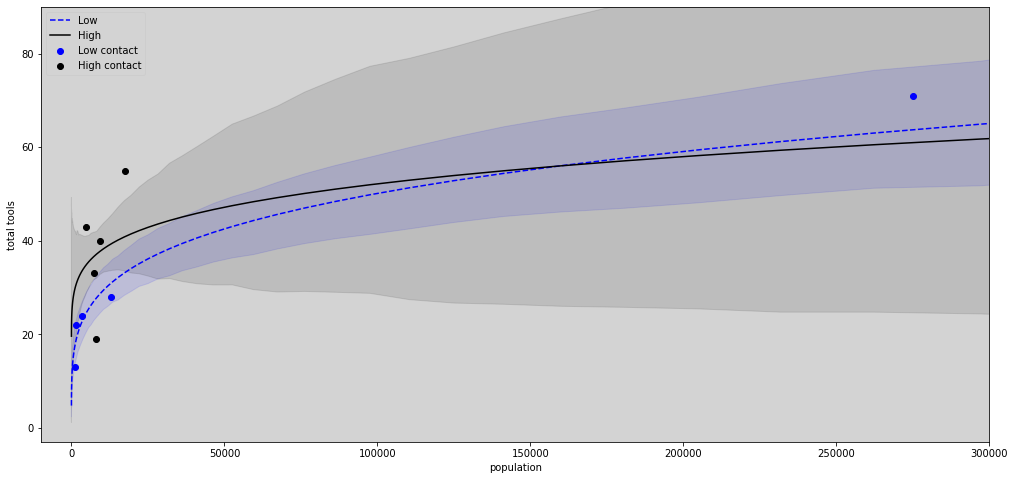
R Code 11.49 - Overthinking: Modeling tool innovation - Pg 356¶

Expected number of tools in one time step is:

\[ \Delta T = \alpha P^\beta - \gamma T \]

\(T\): Number of tools
\(\alpha, \beta, \gamma\): Parameters to be estimated

The equilibrium number of tools \(T\), just \(\Delta T = 0\) and solve for T.

\[ \hat{T} = \frac{\alpha P^\beta}{\gamma} \]

The noise around the outcome will still be \(Poisson\), because that is still maximum entropy distribution in this context - total_tools is a count with no clear upper bound. The linear model is:

\[ T_i \sim Poisson(\lambda_i) \]

\[ \lambda_i = \frac{\alpha P^\beta_i}{\gamma} \]

N = 100

p_seq = np.linspace(df.log_population.min(), df.log_population.max(), N)

a = np.random.normal(1, 1, N)
b = np.random.exponential(1, N)
g = np.random.exponential(1, N)

plt.figure(figsize=(17, 6))

plt.hist(a, alpha=0.3, label='alpha')
plt.hist(b, alpha=0.3, label='beta')
plt.hist(g, alpha=0.3, label='gamma')

plt.legend(loc='upper right')
plt.show()

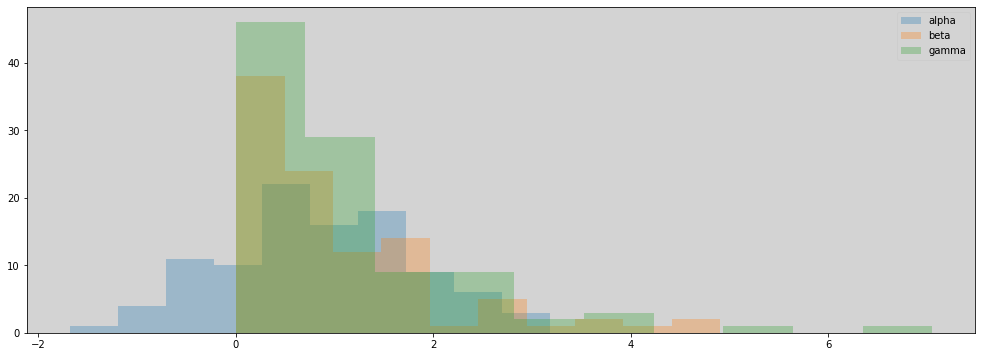
np.shape(lambda_[0])

()

plt.figure(figsize=(17, 6))

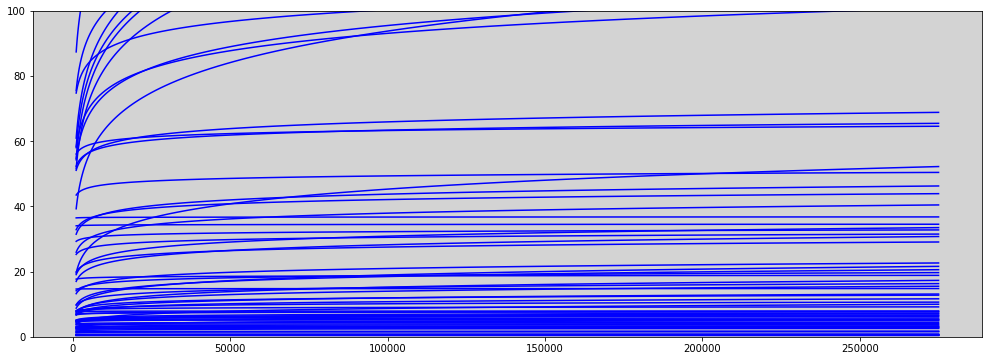
lambda_ = [(np.exp(a[i]) * (p_seq ** b[i])) / g[i] for i in range(N)] 

for i in range(N):
    plt.plot(p_seq, lambda_[i], c='blue')
    
plt.ylim(0, 100)
plt.show()

plt.figure(figsize=(17, 6))
for i in range(N):
    plt.plot(np.exp(p_seq), lambda_[i], c='blue')
    
plt.ylim(0, 100)
plt.show()

model = """
    data {
        int N;
        int qty_cid;
        array[N] int total_tools;
        array[N] real population;
        array[N] int contact_id;
    }
    
    parameters {
        array[qty_cid] real alpha;
        array[qty_cid] real<lower=0> beta;
        real<lower=0> gamma;
    }
    
    model {
        array[N] real lambda;
        
        // Prioris
        alpha ~ normal(1, 1);
        beta ~ exponential(1);
        gamma ~ exponential(1);
        
        for(i in 1:N){
            lambda[i] = (exp(alpha[ contact_id[i] ]) * population[i] ^ beta[ contact_id[i] ])/gamma;
        }
        
        //likelihood
        total_tools ~ poisson(lambda);
    }
"""

data_list = df[["total_tools", "contact_id", "population"]].to_dict('list')
data_list['N'] = len(df.total_tools)
data_list['qty_cid'] = len(df.contact_id.unique())

posteriori = stan.build(model, data=data_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_11_11 = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
    observed_data=list(data_list.keys()),
    dims = {
        'alpha': ['contact_id'],
        'beta': ['contact_id'],
    }
)

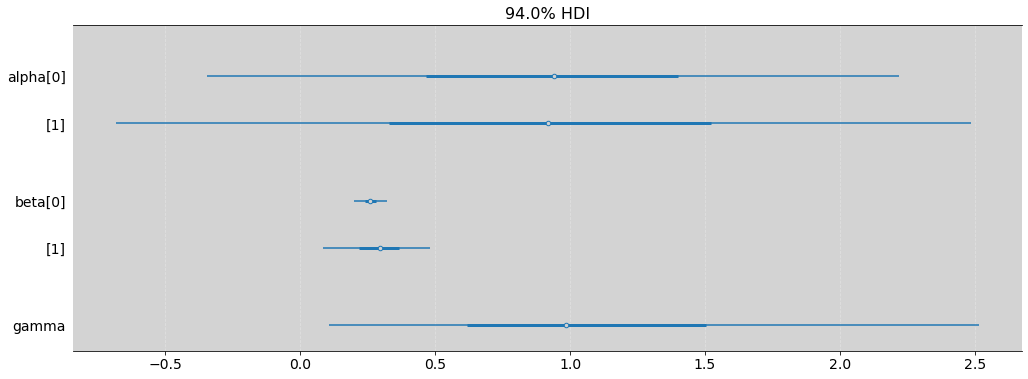
az.summary(model_11_11)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	0.917	0.685	-0.346	2.219	0.017	0.012	1681.0	1625.0	1.01
alpha[1]	0.922	0.857	-0.682	2.488	0.020	0.015	1923.0	1648.0	1.00
beta[0]	0.261	0.033	0.198	0.323	0.001	0.000	2336.0	1623.0	1.00
beta[1]	0.292	0.106	0.084	0.481	0.003	0.002	1601.0	1392.0	1.00
gamma	1.164	0.776	0.107	2.514	0.019	0.013	1518.0	1454.0	1.00

az.plot_forest(model_11_11, var_names=['alpha', 'beta', 'gamma'], combined=True, figsize=(17, 6))

plt.grid(axis='x', color='white', alpha=0.3, ls='--')

plt.show()

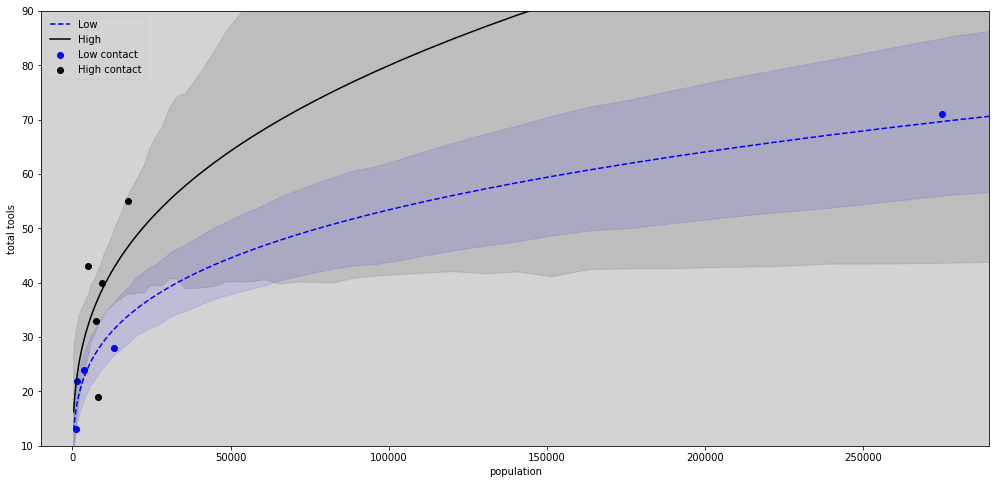
N = 100
a_low = model_11_11.posterior.alpha.sel(contact_id=0).values.flatten()  # CID = 0 (low contact) 
b_low = model_11_11.posterior.beta.sel(contact_id=0).values.flatten()  # CID = 0 (low contact)

a_high = model_11_11.posterior.alpha.sel(contact_id=1).values.flatten()  # CID = 1 (high contact) 
b_high = model_11_11.posterior.beta.sel(contact_id=1).values.flatten()  # CID = 1 (high contact)

g = model_11_11.posterior.gamma.values.flatten()


p_seq = np.linspace(df.log_population.min() -1 , df.log_population.max() + 1, N)

pop_seq = np.exp(p_seq)

lambda_poisson_low =  np.array([ (np.exp(a_low) * pop_seq[i] ** b_low)/g for i in range(N)])
hdi_low = np.transpose([ az.hdi(lambda_poisson_low[i]) for i in range(N) ])
            
lambda_poisson_high =  np.array([ (np.exp(a_high) * pop_seq[i] ** b_high)/g for i in range(N)])
hdi_high = np.transpose([ az.hdi(lambda_poisson_high[i]) for i in range(N) ])

plt.figure(figsize=(17,8))

plt.plot(pop_seq,lambda_poisson_low.mean(axis=1), c='blue', label='Low', ls='--')  # Low
plt.fill_between(pop_seq, hdi_low[0], hdi_low[1], color='blue', alpha=0.1)

plt.plot(pop_seq, lambda_poisson_high.mean(axis=1), c='black', label='High')  # High
plt.fill_between(pop_seq, hdi_high[0], hdi_high[1], color='black', alpha=0.1)

# Plot the points
plt.scatter(df[df['contact_id'] == 1].population, df[df['contact_id'] == 1].total_tools, label='Low contact', color='blue')
plt.scatter(df[df['contact_id'] == 2].population, df[df['contact_id'] == 2].total_tools, label='High contact', color='black')

# Limits graphs
plt.xlim(-10000, 290000)
plt.ylim(10, 90)

plt.title('')
plt.xlabel('population')
plt.ylabel('total tools')
plt.legend(loc='upper left')

plt.show()

Example: Exposure and the offset:¶

Implicity, \(\lambda\) is equal to an expexted number of events, \(\mu\), per unit time or distance, \(\tau\).

This implies that \(\lambda = \frac{\mu}{\tau}\).

\[ y_i \sim Poisson(\lambda_i) \]

\[ log \lambda_i = log \frac{\mu_i}{\tau_i} = \alpha + \beta x_i \]

\[ log \mu_i = \log \tau_i + \alpha + \beta x_i \]

The \(\tau\) values are the “\(exposures\)”. When \(\tau_i=1\), then \(log(\tau_i) = 0\) and we’re back where we started.

Then the model with different exposures just by writing a model like:

\[ y_i \sim Poisson(\mu_i) \]

\[ log \mu_i = log \tau_i + \alpha + \beta x_i \]

R Code 11.50¶

num_days = 30

y = np.random.poisson(lam=1.5 ,size=num_days)
y

array([4, 0, 0, 4, 3, 0, 2, 2, 2, 5, 0, 1, 3, 1, 4, 3, 3, 3, 3, 1, 2, 0,
       1, 1, 2, 1, 3, 4, 0, 0])

R Code 11.51¶

num_weeks = 4

y_new = np.random.poisson(lam=0.5*7, size=num_weeks)
y_new

array([4, 2, 3, 3])

R Code 11.52¶

y_all = np.concatenate([y, y_new])
exposure = np.concatenate([np.repeat(1, 30), np.repeat(7, 4)])
monastery = np.concatenate([np.repeat(0, 30), np.repeat(1, 4)])

df = pd.DataFrame.from_dict(dict(y=y_all, days=exposure, monastery=monastery))
df

	y	days	monastery
0	4	1	0
1	0	1	0
2	0	1	0
3	4	1	0
4	3	1	0
5	0	1	0
6	2	1	0
7	2	1	0
8	2	1	0
9	5	1	0
10	0	1	0
11	1	1	0
12	3	1	0
13	1	1	0
14	4	1	0
15	3	1	0
16	3	1	0
17	3	1	0
18	3	1	0
19	1	1	0
20	2	1	0
21	0	1	0
22	1	1	0
23	1	1	0
24	2	1	0
25	1	1	0
26	3	1	0
27	4	1	0
28	0	1	0
29	0	1	0
30	4	7	1
31	2	7	1
32	3	7	1
33	3	7	1

R Code 11.52¶

model = """
    data {
        int N;
        array[N] int y;
        array[N] real log_days;
        array[N] int monastery;
    }
    
    parameters {
        real alpha;
        real beta;
    }
    
    model {
        array[N] real lambda;
        
        alpha ~ normal(0, 1);
        beta ~ normal(0, 1);
        
        for (i in 1:N){
            lambda[i] = log_days[i] + alpha + monastery[i] * beta ;
            lambda[i] = exp(lambda[i]);
        }
        
        y ~poisson(lambda);
    }
"""

df['log_days'] = np.log(df['days'])

data_list = df[['y', 'log_days', 'monastery']].to_dict('list')
data_list['N'] = len(df)

posteriori = stan.build(model, data=data_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_11_12 = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
    observed_data=list(data_list.keys())
)

R Code 11.54¶

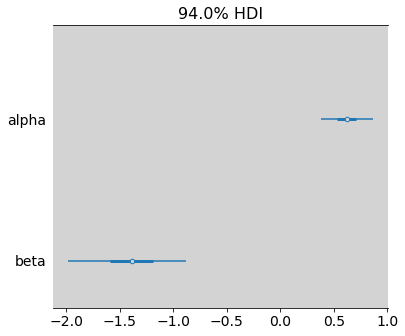
az.plot_forest(model_11_12, var_names=["alpha", "beta"], combined=True)
plt.show()

alpha = model_11_12.posterior.alpha
beta = model_11_12.posterior.beta

lambda_old = np.exp(alpha)
lambda_new = np.exp(alpha + beta)


az.plot_forest(lambda_old, var_names=['alpha'], combined=True)
plt.show()
az.summary(lambda_old)

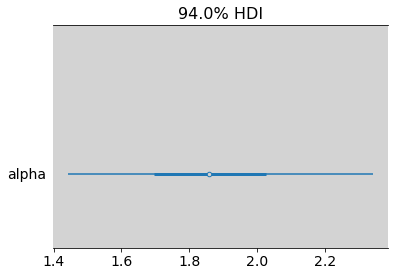
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	1.871	0.244	1.444	2.34	0.005	0.004	2097.0	1945.0	1.0

az.plot_forest(lambda_new, combined=True)
plt.show()

az.summary(lambda_new)

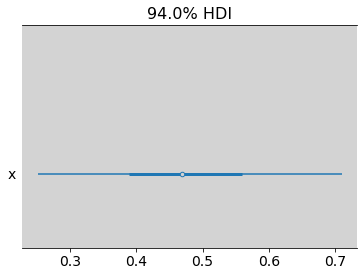
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
x	0.479	0.126	0.251	0.71	0.002	0.002	3170.0	2567.0	1.0

Predictors matched to outcomes¶

def softmax(scores_list):
    return np.exp(scores_list) / np.sum(np.exp(scores_list))

R Code 11.55¶

# Simulate career choices among 500 individuals

N = 500  # number individuals
income = np.array([1, 2, 5])  # expected income of each career
score = income * 0.5  # scores for each career, based on income

# next line converts scores to probabilities
p = softmax([score[0], score[1], score[2]])

career = [np.random.choice([1, 2, 3], size=1, p=p)[0] for _ in range(N)]

print('Career choiced: ', career[:20], '\nIncome: ', income, '\nScore:  ', score)

Career choiced:  [2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 3, 2, 2, 3, 3, 3] 
Income:  [1 2 5] 
Score:   [0.5 1.  2.5]

R Code 11.56¶

model = """
    data {
        int N;  // number of individuals - Here is 500
        int K;  // number of possible careers - Here is 3
        
        array[N] int career;  // outcome
        vector[K]  career_income;
    }
    
    parameters {
        vector[K-1] a;  // intercepts
        real<lower=0> b;  // association of income with choice
    }
    
    model {
        vector[K] p;
        vector[K] s;
        
        a ~ normal(0, 1);
        b ~ normal(0, 0.5);
        
        s[1] = a[1] + b * career_income[1];
        s[2] = a[2] + b * career_income[2];
        s[3] = 0;  // pivot
        
        p = softmax( s );
        
        career ~ categorical(p);
    }
"""

dat_list = dict({
    'N': len(career), # 500
    'K': len(score),  # 3
    'career': career,
    'career_income': income,
})

posteriori = stan.build(model, data=dat_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

R Code 11.57¶

np.std(samples['a'][0])

0.16525252892399064

model_11_13 = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
    observed_data=list(dat_list.keys()),
)

az.summary(model_11_13)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a[0]	-2.073	0.165	-2.423	-1.808	0.007	0.005	668.0	608.0	1.01
a[1]	-1.730	0.216	-2.145	-1.361	0.011	0.008	436.0	429.0	1.00
b	0.122	0.096	0.000	0.299	0.005	0.004	431.0	569.0	1.00

obs: This model not fitting like a book!

TODO: Read this in future!

Explanations: https://github.com/pymc-devs/pymc-resources/blob/main/Rethinking_2/Chp_11.ipynb

The model described in the book does not sample well in PyMC. It does slightly better if we change the pivot category to be the first career instead of the third, but this is still suboptimal because we are discarding predictive information from the pivoted category (i.e., its unique career income).

In fact, it is not necessary to pivot the coefficients of variables that are distinct for each category (what the author calls predictors matched to outcomes), as it is done for the coefficients of shared variables (what the author calles predictors matched to observations). The intercepts belong to the second category, and as such they still need to be pivoted. These two references explain this distinction clearly:

Hoffman, S. D., & Duncan, G. J. (1988). Multinomial and conditional logit discrete-choice models in demography. Demography, 25(3), 415-427 pdf link Croissant, Y. (2020). Estimation of Random Utility Models in R: The mlogit Package. Journal of Statistical Software, 95(1), 1-41 pdf pdf link

R Code 11.58¶

a = model_11_13.posterior.a
b = model_11_13.posterior.b


s1 = (a.sel(a_dim_0=0) + b * income[0]).values.flatten()
s2_old = (a.sel(a_dim_0=1) + b * income[1]).values.flatten()
s2_new = (a.sel(a_dim_0=1) + b * income[1] * 2).values.flatten()

p_orig = [softmax([s1[i], s2_old[i], 0]) for i in range(len(s1)) ]
p_new  = [softmax([s1[i], s2_new[i], 0]) for i in range(len(s1)) ]

# Summarize
p_diff = np.transpose(p_new)[1] - np.transpose(p_orig)[1]

az.plot_forest([np.transpose(p_new)[1], np.transpose(p_orig)[1], p_diff], model_names=['new', 'old', 'diff_new_to_old'])
plt.show()

az.summary(p_diff)

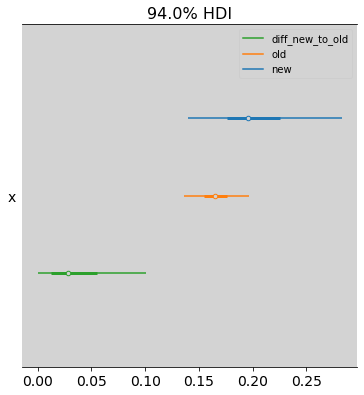
arviz - WARNING - Shape validation failed: input_shape: (1, 4000), minimum_shape: (chains=2, draws=4)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
x	0.038	0.033	0.0	0.101	0.002	0.001	436.0	554.0	NaN

So on average a \(5\%\) increase in probability of choosing the career, when the income is doubled.

Predictors Matched to observations (pg 362)¶

R Code 11.59¶

N = 500

# Simulate family incomes for each individual
family_income = np.random.uniform(0, 1, N)

b = np.array([-2, 0, 2])
career = np.empty(N)

for i in range(N):
    score = np.array([1, 2, 3]) * 0.5 + b * family_income[i]
    p = softmax([score[0], score[1], score[2]])
    career[i] = np.random.choice([1, 2, 3], size=1, p=p)
    
career = career.astype(int)
print('Career choiced: ', career[:15])
print('Family Income: ', family_income[:5])

Career choiced:  [3 3 1 3 3 3 3 2 3 3 2 3 2 3 3]
Family Income:  [0.88220597 0.26090131 0.41481564 0.95091294 0.31800893]

model = """
    data{
        int N;
        int K;
        array[N] int career;
        array[N] real family_income;
    }
    
    parameters {
        vector[K-1] a; // intercepts
        vector[K-1] b; // coefficients on family income
    }
    
    model {
        vector[K] p;
        vector[K] s;
        
        a ~ normal(1, 1.5);
        b ~ normal(0, 1);
        
        for (i in 1:N) {
            for (j in 1:(K-1)) s[j] = a[j] + b[j]*family_income[i];
            s[K] = 0;
            p = softmax( s );
            career[i] ~ categorical( p );
        }
    }
"""

dat_list = {
    'N': N,
    'K': len(b),
    'career': career,
    'family_income': family_income,
}

posteriori = stan.build(model, data=dat_list)
samples = posteriori.sample(num_chains=4, num_samples=1000)

model_11_14 = az.from_pystan(
    posterior=samples,
    posterior_model=posteriori,
)

az.summary(model_11_14)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a[0]	-1.306	0.266	-1.802	-0.812	0.006	0.004	2149.0	2219.0	1.0
a[1]	-0.639	0.201	-1.019	-0.270	0.004	0.003	2279.0	2078.0	1.0
b[0]	-2.276	0.550	-3.329	-1.255	0.012	0.008	2176.0	2278.0	1.0
b[1]	-1.536	0.383	-2.263	-0.826	0.008	0.006	2294.0	1994.0	1.0

Multinomial disguise as Poisson¶

R Code 11.60¶

df = pd.read_csv('./data/UCBadmit.csv', sep=';')
df

	dept	applicant.gender	admit	reject	applications
1	A	male	512	313	825
2	A	female	89	19	108
3	B	male	353	207	560
4	B	female	17	8	25
5	C	male	120	205	325
6	C	female	202	391	593
7	D	male	138	279	417
8	D	female	131	244	375
9	E	male	53	138	191
10	E	female	94	299	393
11	F	male	22	351	373
12	F	female	24	317	341

df.admit.values

array([512,  89, 353,  17, 120, 202, 138, 131,  53,  94,  22,  24])

model_bin = """
    data{
        int N;
        array[N] int admit;
        array[N] int applications;
    }
    
    parameters {
        real a;
    }
    
    model {
        real p;
        
        a ~ normal(0, 1.5);
        p = inv_logit(a);
        
        admit ~ binomial(applications, p);
    }
"""

dat_list_bin = {
    'N': len(df),
    'admit': df.admit.values,
    'applications': df.applications.values,
}

posteriori_bin = stan.build(model_bin, data=dat_list_bin)
samples_bin = posteriori_bin.sample(num_chains=4, num_samples=1000)

m_bin = az.from_pystan(
    posterior=samples_bin,
    posterior_model=posteriori_bin 
)

R Code 11.62¶

az.plot_forest(
    m_bin,
    var_names=['a'],
    combined=True,
    transform=inv_logit,
    figsize=(17, 3),
    hdi_prob=0.89,
)
plt.show()

az.summary(inv_logit(m_bin.posterior.a))

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a	0.388	0.007	0.374	0.402	0.0	0.0	1343.0	1691.0	1.0

# RCode 11.61 - Poisson model

model_poi = """
    data{
        int N;
        array[N] int admit;
        array[N] int rej;
        array[N] int applications;
    }
    
    parameters {
        real a1;
        real a2;
    }
    
    model {
        real lambda_1;
        real lambda_2;
        
        a1 ~ normal(0, 1.5);
        a2 ~ normal(0, 1.5);
        
        lambda_1 = exp(a1);
        lambda_2 = exp(a2);
        
        admit ~ poisson(lambda_1);
        rej ~ poisson(lambda_2);
    }
"""

dat_list_poi = {
    'N': len(df),
    'admit': df.admit.values,
    'rej': df.reject.values,
    'applications': df.applications.values,
}

posteriori_poi = stan.build(model_poi, data=dat_list_poi)
samples_poi = posteriori_poi.sample(num_chains=4, num_samples=1000)

m_poi = az.from_pystan(
    posterior=samples_poi,
    posterior_model=posteriori_poi 
)

R Code 11.63¶

lam1 = np.exp(m_poi.posterior.a1)
lam2 = np.exp(m_poi.posterior.a2)

resp = lam1 / (lam1 + lam2)

az.plot_forest(resp, 
               combined=True,
               figsize=(17, 3),
               hdi_prob=0.89)
plt.show()

az.summary(resp)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
x	0.388	0.007	0.374	0.401	0.0	0.0	3787.0	2203.0	1.0

	actor	recipient	block	trial	prosoc_left	chose_prosoc	pulled_left	treatment
0	1	NaN	1	2	0	1	0	1
1	1	NaN	1	4	0	0	1	1
2	1	NaN	1	6	1	0	0	2
3	1	NaN	1	8	0	1	0	1
4	1	NaN	1	10	1	1	1	2

	y	days	monastery
0	4	1	0
1	0	1	0
2	0	1	0
3	4	1	0
4	3	1	0
5	0	1	0
6	2	1	0
7	2	1	0
8	2	1	0
9	5	1	0
10	0	1	0
11	1	1	0
12	3	1	0
13	1	1	0
14	4	1	0
15	3	1	0
16	3	1	0
17	3	1	0
18	3	1	0
19	1	1	0
20	2	1	0
21	0	1	0
22	1	1	0
23	1	1	0
24	2	1	0
25	1	1	0
26	3	1	0
27	4	1	0
28	0	1	0
29	0	1	0
30	4	7	1
31	2	7	1
32	3	7	1
33	3	7	1

	actor	recipient	block	trial	prosoc_left	chose_prosoc	pulled_left	treatment
0	1	NaN	1	2	0	1	0	1
1	1	NaN	1	4	0	0	1	1
2	1	NaN	1	6	1	0	0	2
3	1	NaN	1	8	0	1	0	1
4	1	NaN	1	10	1	1	1	2

	y	days	monastery
0	4	1	0
1	0	1	0
2	0	1	0
3	4	1	0
4	3	1	0
5	0	1	0
6	2	1	0
7	2	1	0
8	2	1	0
9	5	1	0
10	0	1	0
11	1	1	0
12	3	1	0
13	1	1	0
14	4	1	0
15	3	1	0
16	3	1	0
17	3	1	0
18	3	1	0
19	1	1	0
20	2	1	0
21	0	1	0
22	1	1	0
23	1	1	0
24	2	1	0
25	1	1	0
26	3	1	0
27	4	1	0
28	0	1	0
29	0	1	0
30	4	7	1
31	2	7	1
32	3	7	1
33	3	7	1

Statistical Rethinking

11 - A cravada de Deus e Inteiros¶

R Code 11.1¶

R Code 11.2¶

R Code 11.3¶

R Code 11.4¶

R Code 11.5¶

R Code 11.6¶

R Code 11.7¶

R Code 11.8¶

R Code 11.9¶

R Code 11.10¶

R Code 11.11¶

R Code 11.12¶

R Code 11.13¶

R Code 8.14¶

R Code 11.15¶

R Code 11.16 and R Code 11.17¶

R Code 11.18¶

R Code 11.19¶

R Code 11.21¶

R Code 11.22¶

R Code 11.23¶

R Code 11.24¶

R Code 11.25¶

R Code 11.26¶

R Code 11.27¶

My Tests¶

R Code 11.28¶

R Code 11.29¶

R Code 11.30¶

R Code 11.31¶

R Code 11.32¶

R Code 11.33¶

Poisson Regression¶

R Code 11.35¶

R Code 11.36¶

R Code 11.37¶

Model - Poisson Regression¶

R Code 11.38¶

R Code 11.39¶

R Code 11.40¶

R Code 11.41¶

R Code 11.42¶

R Code 11.43¶

R Code 11.44¶

Curiosidade do python¶

R Code 11.45¶

Model:¶

Model:¶

R Code 11.46¶

R Code 11.47¶

R Code 11.48¶

R Code 11.49 - Overthinking: Modeling tool innovation - Pg 356¶

Example: Exposure and the offset:¶

R Code 11.50¶

R Code 11.51¶

R Code 11.52¶

R Code 11.52¶

R Code 11.54¶

Predictors matched to outcomes¶

R Code 11.55¶

R Code 11.56¶

R Code 11.57¶

R Code 11.58¶

Predictors Matched to observations (pg 362)¶

R Code 11.59¶

Multinomial disguise as Poisson¶

R Code 11.60¶

R Code 11.62¶

R Code 11.63¶

	actor	recipient	block	trial	prosoc_left	chose_prosoc	pulled_left	treatment
0	1	NaN	1	2	0	1	0	1
1	1	NaN	1	4	0	0	1	1
2	1	NaN	1	6	1	0	0	2
3	1	NaN	1	8	0	1	0	1
4	1	NaN	1	10	1	1	1	2

	y	days	monastery
0	4	1	0
1	0	1	0
2	0	1	0
3	4	1	0
4	3	1	0
5	0	1	0
6	2	1	0
7	2	1	0
8	2	1	0
9	5	1	0
10	0	1	0
11	1	1	0
12	3	1	0
13	1	1	0
14	4	1	0
15	3	1	0
16	3	1	0
17	3	1	0
18	3	1	0
19	1	1	0
20	2	1	0
21	0	1	0
22	1	1	0
23	1	1	0
24	2	1	0
25	1	1	0
26	3	1	0
27	4	1	0
28	0	1	0
29	0	1	0
30	4	7	1
31	2	7	1
32	3	7	1
33	3	7	1