8 - Os peixes-bois condicionais¶

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

import pandas as pd

import networkx as nx
# from causalgraphicalmodels import CausalGraphicalModel

import arviz as az
# ArviZ ships with style sheets!
# https://python.arviz.org/en/stable/examples/styles.html#example-styles
az.style.use("arviz-darkgrid")

import xarray as xr

import stan
import nest_asyncio

plt.style.use('default')
plt.rcParams['axes.facecolor'] = 'lightgray'

# To DAG's
import daft
from causalgraphicalmodels import CausalGraphicalModel

# Add fonts to matplotlib to run xkcd

from matplotlib import font_manager

font_dirs = ["fonts/"]  # The path to the custom font file.
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)

for font_file in font_files:
    font_manager.fontManager.addfont(font_file)

# plt.xkcd()

# To running the stan in jupyter notebook
nest_asyncio.apply()

R Code 8.1¶

df = pd.read_csv('./data/rugged.csv', sep=';')
df.head()

	isocode	isonum	country	rugged	rugged_popw	rugged_slope	rugged_lsd	rugged_pc	land_area	lat	...	africa_region_c	slave_exports	dist_slavemkt_atlantic	dist_slavemkt_indian	dist_slavemkt_saharan	dist_slavemkt_redsea	pop_1400	european_descent
0	ABW	533	Aruba	0.462	0.380	1.226	0.144	0.000	18.0	12.508	...	0	0.0	NaN	NaN	NaN	NaN	614.0	NaN
1	AFG	4	Afghanistan	2.518	1.469	7.414	0.720	39.004	65209.0	33.833	...	0	0.0	NaN	NaN	NaN	NaN	1870829.0	0.0
2	AGO	24	Angola	0.858	0.714	2.274	0.228	4.906	124670.0	-12.299	...	1	3610000.0	5.669	6.981	4.926	3.872	1223208.0	2.0
3	AIA	660	Anguilla	0.013	0.010	0.026	0.006	0.000	9.0	18.231	...	0	0.0	NaN	NaN	NaN	NaN	NaN	NaN
4	ALB	8	Albania	3.427	1.597	10.451	1.006	62.133	2740.0	41.143	...	0	0.0	NaN	NaN	NaN	NaN	200000.0	100.0

5 rows × 51 columns

df['log_gdp'] = np.log(df['rgdppc_2000'])  # Log version of outcome
df[['rgdppc_2000', 'log_gdp']].head()

	rgdppc_2000	log_gdp
0	NaN	NaN
1	NaN	NaN
2	1794.729	7.492609
3	NaN	NaN
4	3703.113	8.216929

ddf = df[~np.isnan(df['log_gdp'].values)].copy()

ddf['log_gdp_std'] = ddf['log_gdp'] / np.mean(ddf['log_gdp'])
ddf['rugged_std'] = ddf['rugged'] / np.max(ddf['rugged'])

ddf[['log_gdp_std', 'rugged_std']]

	log_gdp_std	rugged_std
2	0.879712	0.138342
4	0.964755	0.552564
7	1.166270	0.123992
8	1.104485	0.124960
9	0.914904	0.433409
...	...	...
229	0.996681	0.270397
230	0.783032	0.374557
231	1.074365	0.283941
232	0.780967	0.085940
233	0.918589	0.192519

170 rows × 2 columns

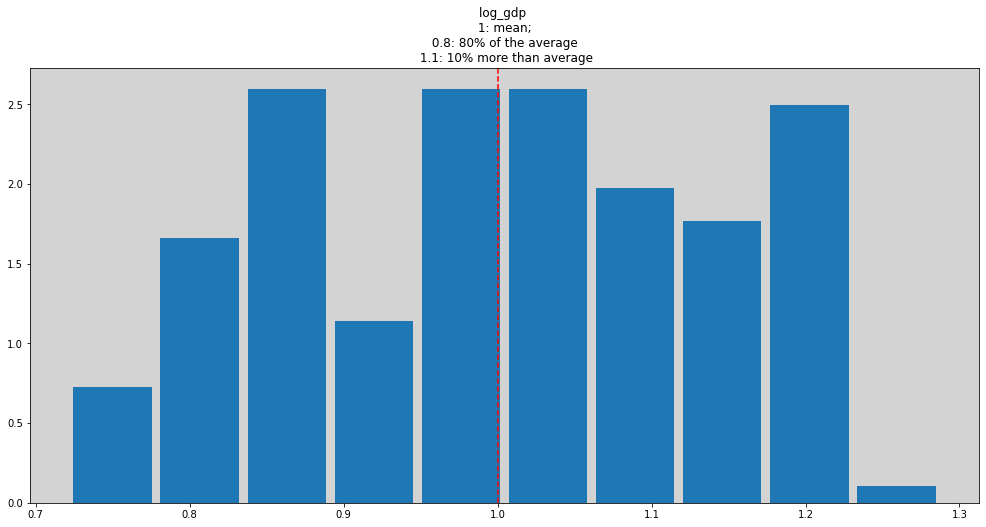
plt.figure(figsize=(17, 8))

plt.hist(ddf['log_gdp_std'], density=True, rwidth=0.9)
plt.title('log_gdp \n 1: mean; \n 0.8: 80% of the average \n 1.1: 10% more than average')
plt.axvline(x=1, c='r', ls='--')
plt.show()

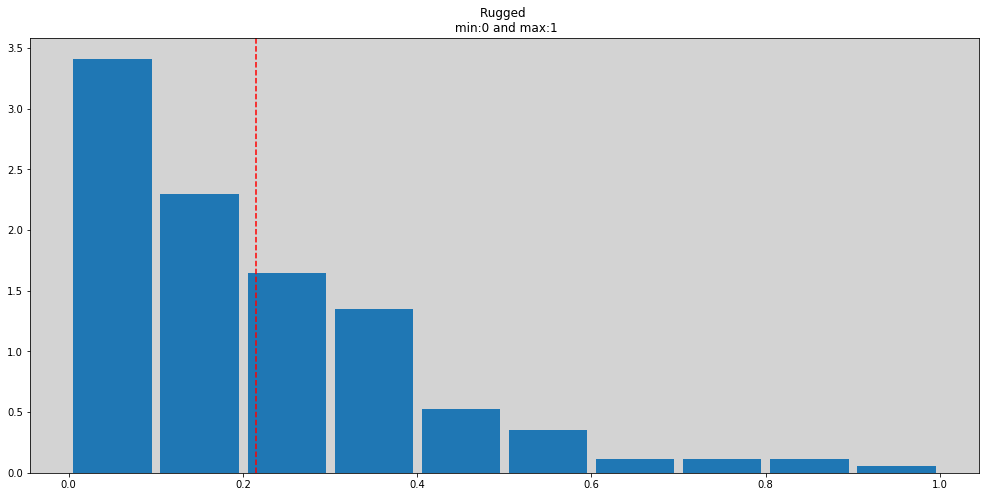
plt.figure(figsize=(17, 8))
plt.hist(ddf['rugged_std'], density=True, rwidth=0.9)
plt.title('Rugged \n min:0 and max:1')
plt.axvline(x=np.mean(ddf['rugged_std']), c='r', ls='--')
plt.show()

R Code 8.2¶

model = """
    data {
        int N;
        vector[N] log_gdp_std;
        vector[N] rugged_std;
        real rugged_std_average;
    }
    
    parameters {
        real alpha;
        real beta;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta * (rugged_std - rugged_std_average);
    }
    
    model {
        // Prioris
        
        alpha ~ normal(1, 1);
        beta ~ normal(0, 1);
        sigma ~ exponential(1);
        
        // Likelihood
        log_gdp_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;  // By default, if a variable log_lik is present in the Stan model, it will be retrieved as pointwise log likelihood values.
        vector[N] log_gdp_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(log_gdp_std[i] | mu[i], sigma);
            log_gdp_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(ddf),
    'log_gdp_std': ddf['log_gdp_std'].values,
    'rugged_std': ddf['rugged_std'].values,
    'rugged_std_average': ddf['rugged_std'].mean(),
}

posteriori = stan.build(model, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

# Transform to dataframe pandas
df_samples = samples.to_frame()
df_samples.head()

parameters	lp__	accept_stat__	stepsize__	treedepth__	n_leapfrog__	divergent__	energy__	alpha	beta	sigma	...	log_gdp_std_hat.161	log_gdp_std_hat.162	log_gdp_std_hat.163	log_gdp_std_hat.164	log_gdp_std_hat.165	log_gdp_std_hat.166	log_gdp_std_hat.167	log_gdp_std_hat.168	log_gdp_std_hat.169	log_gdp_std_hat.170
draws
0	251.095956	0.934916	0.756421	2.0	3.0	0.0	-249.133644	1.003160	0.012665	0.132500	...	1.034012	0.906565	0.989983	0.945965	1.046566	1.012428	0.871437	0.955593	1.041951	0.856201
1	247.262579	0.989367	0.751819	2.0	3.0	0.0	-246.744846	1.005781	0.135747	0.151454	...	1.044460	1.144566	0.875533	0.860964	1.094581	1.177379	1.083208	1.013122	0.992572	1.167171
2	250.380368	0.998516	0.943934	2.0	7.0	0.0	-249.945732	1.002515	0.032714	0.128198	...	1.047150	1.007480	1.019530	1.052204	1.112828	1.149602	1.175402	1.279579	1.000648	0.870344
3	250.516786	0.913792	0.862509	2.0	3.0	0.0	-249.646704	1.002620	0.045010	0.130002	...	1.144794	0.994287	1.006064	1.133213	0.878218	1.246487	0.956800	0.669329	1.084075	0.973772
4	247.927975	0.574694	0.756421	2.0	3.0	0.0	-246.256142	1.018086	-0.077998	0.129151	...	0.921305	0.814742	0.918643	0.982626	0.949444	0.886278	1.159055	0.902815	0.837451	1.115775

5 rows × 520 columns

# stan_fit to arviz_stan

stan_data = az.from_pystan(
    posterior=samples,
    posterior_predictive="log_gdp_std_hat",
    observed_data=['log_gdp_std'],
    prior=samples,
    prior_model=posteriori,
    posterior_model=posteriori,
)

az.summary(stan_data, var_names=['alpha', 'beta', 'sigma'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	1.000	0.010	0.980	1.019	0.000	0.000	4227.0	2654.0	1.0
beta	0.002	0.056	-0.097	0.113	0.001	0.001	3467.0	2810.0	1.0
sigma	0.138	0.008	0.125	0.153	0.000	0.000	3838.0	2808.0	1.0

R Code 8.3¶

plt.figure(figsize=(17, 8))

alpha = np.random.normal(1, 1, 1000)
beta = np.random.normal(0, 1, 1000)

rugged_seq = np.linspace(0, 1, 100)

for i in range(100):
    plt.plot(rugged_seq, alpha[i] + beta[i] * rugged_seq, c='blue')
    
plt.axhline(y=1.3, c='r', ls='--')    
plt.axhline(y=0.7, c='r', ls='--')    
    
plt.ylim((0.5, 1.5))
plt.title('Using vague priors')
plt.xlabel('Ruggedness')
plt.ylabel('Log GDP')

plt.show()

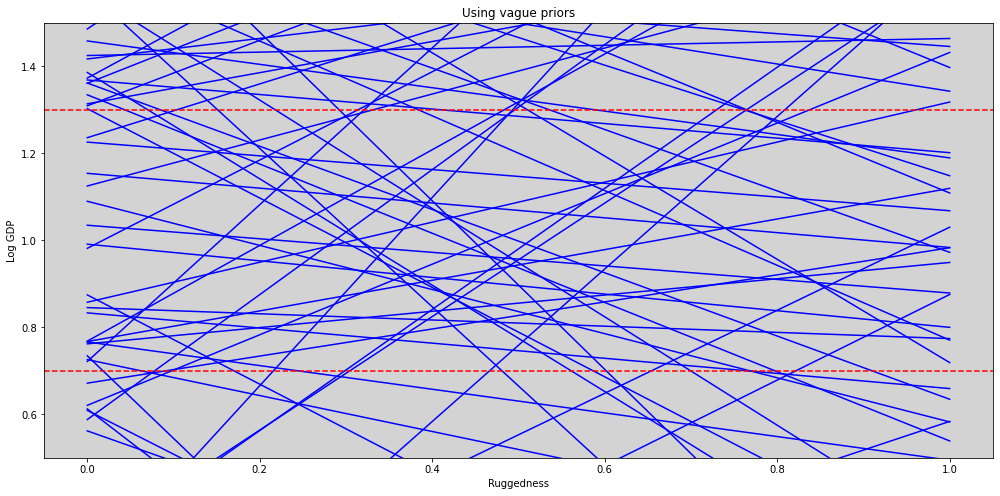
R Code 8.4¶

plt.figure(figsize=(17, 8))

plt.hist(beta, bins=30, rwidth=0.9)
plt.axvline(x=0.6, c='r', ls='--')
plt.axvline(x=-0.6, c='r', ls='--')
plt.show()

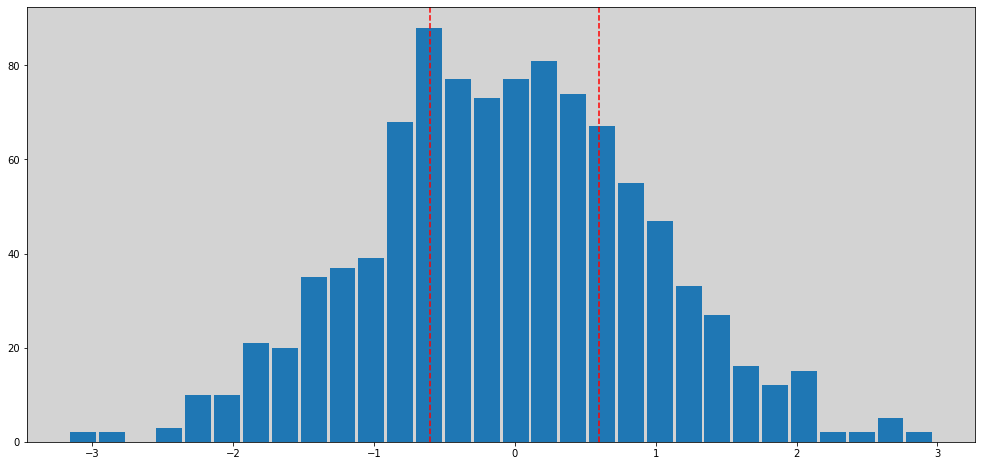
np.sum(np.sum(np.abs(beta) > 0.6) / len(beta))

0.55

R Code 8.5¶

plt.figure(figsize=(17, 8))

alpha = np.random.normal(1, 0.1, 1000)
beta = np.random.normal(0, 0.3, 1000)

rugged_seq = np.linspace(0, 1, 100)

for i in range(100):
    plt.plot(rugged_seq, alpha[i] + beta[i] * rugged_seq, c='blue')
    
plt.axhline(y=1.3, c='r', ls='--')    
plt.axhline(y=0.7, c='r', ls='--')    

plt.ylim((0.5, 1.5))
plt.title('Using a informative prior')
plt.xlabel('Ruggedness')
plt.ylabel('Log GDP')

plt.show()

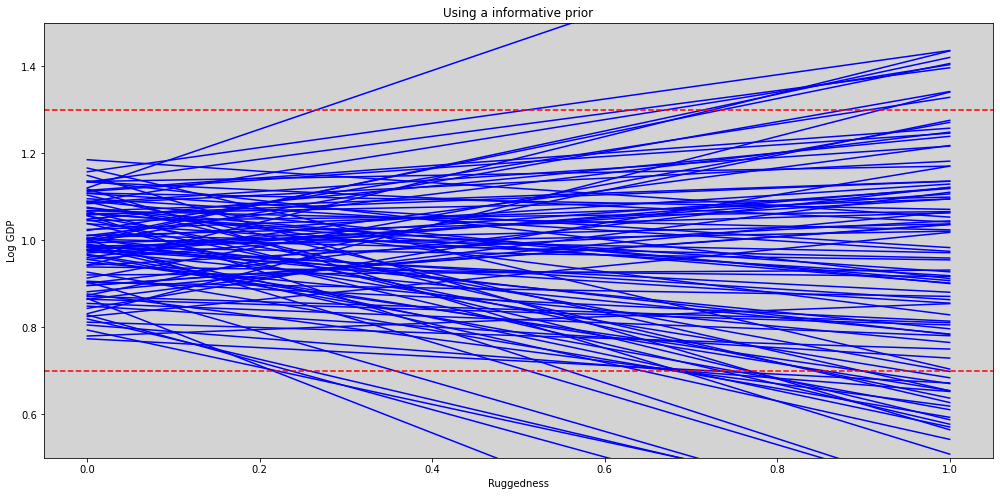
model2 = """
    data {
        int N;
        vector[N] log_gdp_std;
        vector[N] rugged_std;
        real rugged_std_average;
    }
    
    parameters {
        real alpha;
        real beta;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta * (rugged_std - rugged_std_average);
    
    }
    
    model {
        // Prioris
        
        alpha ~ normal(1, 0.1);
        beta ~ normal(0, 0.3);
        sigma ~ exponential(1);
        
        // Likelihood
        log_gdp_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;  // By default, if a variable log_lik is present in the Stan model, it will be retrieved as pointwise log likelihood values.
        vector[N] log_gdp_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(log_gdp_std[i] | mu[i], sigma);
            log_gdp_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(ddf),
    'log_gdp_std': ddf['log_gdp_std'].values,
    'rugged_std': ddf['rugged_std'].values,
    'rugged_std_average': ddf['rugged_std'].mean(),
}

posteriori = stan.build(model2, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

stan_data2 = az.from_pystan(
    posterior=samples,
    posterior_predictive="log_gdp_std_hat",
    observed_data=['log_gdp_std'],
    prior=samples,
    prior_model=posteriori,
    posterior_model=posteriori,
)

az.summary(stan_data, var_names=['alpha', 'beta', 'sigma'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	1.000	0.010	0.980	1.019	0.000	0.000	4227.0	2654.0	1.0
beta	0.002	0.056	-0.097	0.113	0.001	0.001	3467.0	2810.0	1.0
sigma	0.138	0.008	0.125	0.153	0.000	0.000	3838.0	2808.0	1.0

R Code 8.7¶

ddf['cid'] = [1 if cont_africa == 1 else 2 for cont_africa in ddf['cont_africa']]
ddf[['cont_africa', 'cid']].head()

	cont_africa	cid
2	1	1
4	0	2
7	0	2
8	0	2
9	0	2

R Code 8.8¶

model3 = """
    data {
        int N;
        vector[N] log_gdp_std;
        vector[N] rugged_std;
        array[N] int cid;  // Must be integer because this is index to alpha.
        real rugged_std_average;
    }
    
    parameters {
        real alpha[2];  //Can be used to real alpha[2] or array[2] int alpha;
        real beta;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        for (i in 1:N){
            mu[i] = alpha[ cid[i] ] + beta * (rugged_std[i] - rugged_std_average);
        }
    }
    
    model {
        // Prioris
        
        alpha ~ normal(1, 0.1);
        beta ~ normal(0, 0.3);
        sigma ~ exponential(1);
        
        // Likelihood
        log_gdp_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] log_gdp_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(log_gdp_std[i] | mu[i], sigma);
            log_gdp_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(ddf),
    'log_gdp_std': ddf['log_gdp_std'].values,
    'rugged_std': ddf['rugged_std'].values,
    'rugged_std_average': ddf['rugged_std'].mean(),
    'cid': ddf['cid'].values,
}

posteriori = stan.build(model3, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

stan_data3 = az.from_pystan(
    posterior=samples,
    posterior_predictive="log_gdp_std_hat",
    observed_data=['log_gdp_std'],
    prior=samples,
    prior_model=posteriori,
    posterior_model=posteriori,
    dims={
        "alpha": ["africa"],
    },
)

R Code 8.9¶

models_8 = { 'm8.1': stan_data2, 'm8.2': stan_data3 }

az.compare(models_8, ic='waic')

/home/rodolpho/Projects/bayesian/BAYES/lib/python3.8/site-packages/arviz/stats/stats.py:1645: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail. 
See http://arxiv.org/abs/1507.04544 for details
  warnings.warn(

	rank	elpd_waic	p_waic	elpd_diff	weight	se	dse	warning	scale
m8.2	0	126.166124	4.117261	0.000000	0.969256	7.396644	0.000000	True	log
m8.1	1	94.499399	2.491680	31.666725	0.030744	6.463956	7.317875	False	log

R Code 8.10¶

az.summary(stan_data3, var_names=['alpha', 'beta', 'sigma'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	0.880	0.016	0.851	0.911	0.000	0.000	4512.0	3483.0	1.0
alpha[1]	1.049	0.010	1.031	1.069	0.000	0.000	4305.0	2642.0	1.0
beta	-0.046	0.047	-0.130	0.048	0.001	0.001	3508.0	2517.0	1.0
sigma	0.114	0.006	0.103	0.126	0.000	0.000	3742.0	3076.0	1.0

R Code 8.12¶

# Extract 200 samples from arviz-fit to numpy
params_post = az.extract(stan_data3.posterior, num_samples=200)

rugged_seq = np.linspace(0, 1, 30)

log_gdp_mean_africa = []
log_gdp_hdi_africa = []

log_gdp_mean_not_africa = []
log_gdp_hdi_not_africa = []

# Calculation posterior mean and interval HDI
for i in range(len(rugged_seq)):
        log_gdp_africa = params_post.alpha.sel(africa=0) + params_post.beta.values * rugged_seq[i]
        log_gdp_mean_africa.append(np.mean(log_gdp_africa.values))
        log_gdp_hdi_africa.append(az.hdi(log_gdp_africa.values, hdi_prob=0.89))
        
        log_gdp_not_africa = params_post.alpha.sel(africa=1) + params_post.beta.values * rugged_seq[i]
        log_gdp_mean_not_africa.append(np.mean(log_gdp_not_africa.values))
        log_gdp_hdi_not_africa.append(az.hdi(log_gdp_not_africa.values, hdi_prob=0.89))
        
log_gdp_hdi_africa = np.array(log_gdp_hdi_africa)
log_gdp_hdi_not_africa = np.array(log_gdp_hdi_not_africa) 

plt.figure(figsize=(17, 8))

plt.plot(rugged_seq, log_gdp_mean_africa, c='blue')
plt.fill_between(rugged_seq, log_gdp_hdi_africa[:,0], log_gdp_hdi_africa[:,1], color='blue', alpha=0.3)

plt.plot(rugged_seq, log_gdp_mean_not_africa, c='black')
plt.fill_between(rugged_seq, log_gdp_hdi_not_africa[:,0], log_gdp_hdi_not_africa[:,1], color='darkgray', alpha=0.3)

plt.plot(ddf.loc[ddf.cid == 1,'rugged_std'], ddf.loc[ddf.cid==1, 'log_gdp_std'], 'o', markerfacecolor='blue', color='gray')
plt.plot(ddf.loc[ddf.cid == 2,'rugged_std'], ddf.loc[ddf.cid==2, 'log_gdp_std'], 'o', markerfacecolor='none', color='black')

plt.title('m8.4')
plt.xlabel('ruggedness (standardized)')
plt.ylabel('log GDP (as proportion of mean)')

plt.text(0.8, 1.04, 'Not Africa', fontsize='x-large', color='black')
plt.text(0.8, 0.86, 'Africa',  fontsize='x-large', color='darkblue')

plt.show()

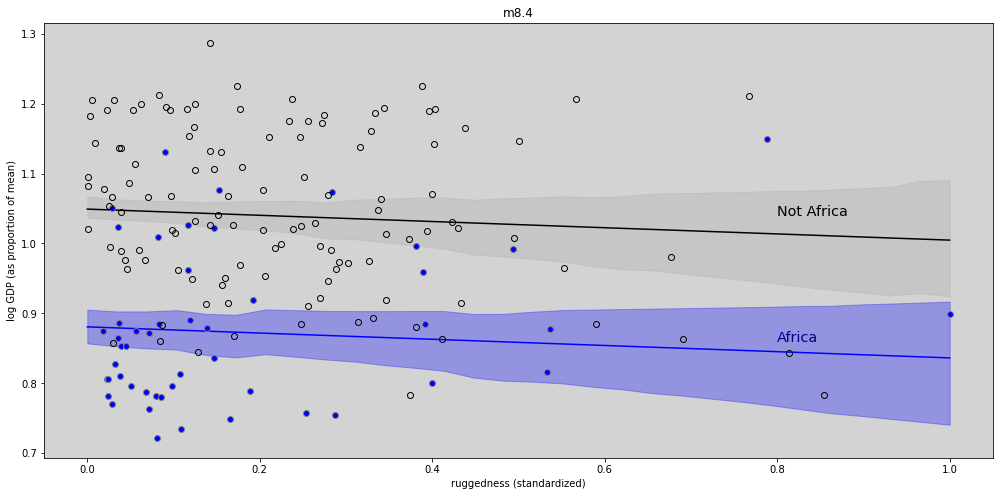
R Code 8.13¶

model4 = """
    data {
        int N;
        vector[N] log_gdp_std;
        vector[N] rugged_std;
        array[N] int cid;  // Must be integer because this is index to alpha.
        real rugged_std_average;
    }
    
    parameters {
        real alpha[2];  //Can be used to real alpha[2] or array[2] int alpha;
        real beta[2];
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        for (i in 1:N){
            mu[i] = alpha[ cid[i] ] + beta[ cid[i] ] * (rugged_std[i] - rugged_std_average);
        }
    }
    
    model {
        // Prioris
        
        alpha ~ normal(1, 0.1);
        beta ~ normal(0, 0.3);
        sigma ~ exponential(1);
        
        // Likelihood
        log_gdp_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] log_gdp_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(log_gdp_std[i] | mu[i], sigma);
            log_gdp_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(ddf),
    'log_gdp_std': ddf['log_gdp_std'].values,
    'rugged_std': ddf['rugged_std'].values,
    'rugged_std_average': ddf['rugged_std'].mean(),
    'cid': ddf['cid'].values,
}

posteriori = stan.build(model4, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

stan_data4 = az.from_pystan(
    posterior=samples,
    posterior_predictive="log_gdp_std_hat",
    observed_data=['log_gdp_std'],
    prior=samples,
    prior_model=posteriori,
    posterior_model=posteriori,
    dims={
        "alpha": ["africa"],
        "beta": ["africa"],
    },
)

R Code 8.14¶

az.summary(stan_data4, var_names=['alpha', 'beta', 'sigma'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha[0]	0.887	0.016	0.858	0.916	0.000	0.000	5156.0	2914.0	1.0
alpha[1]	1.051	0.010	1.033	1.071	0.000	0.000	5063.0	3095.0	1.0
beta[0]	0.131	0.075	-0.006	0.270	0.001	0.001	4710.0	3386.0	1.0
beta[1]	-0.143	0.056	-0.247	-0.036	0.001	0.001	4727.0	3117.0	1.0
sigma	0.112	0.006	0.100	0.123	0.000	0.000	5069.0	3262.0	1.0

R Code 8.15¶

models_8 = { 'm8.1': stan_data2, 'm8.2': stan_data3, 'm8.3': stan_data4 }

# https://python.arviz.org/en/stable/api/generated/arviz.compare.html
# https://rss.onlinelibrary.wiley.com/doi/10.1111/1467-9868.00353
az.compare(models_8, ic='loo')  # loo is same that PSIS

	rank	elpd_loo	p_loo	elpd_diff	weight	se	dse	warning	scale
m8.3	0	129.589277	4.989499	0.000000	0.870793	7.309693	0.000000	False	log
m8.2	1	126.137495	4.145890	3.451783	0.129207	7.405339	3.225278	False	log
m8.1	2	94.492463	2.498616	35.096814	0.000000	6.464447	7.448111	False	log

R Code 8.16 - XXX¶

# az.plot_loo_pit(stan_data4, y='log_gdp_std')

R Code 8.17¶

# Extract 200 samples from arviz-fit to numpy
params_post = az.extract(stan_data4.posterior, num_samples=200)

rugged_seq = np.linspace(0, 1, 30)

log_gdp_mean_africa = []
log_gdp_hdi_africa = []

log_gdp_mean_not_africa = []
log_gdp_hdi_not_africa = []

# Calculation posterior mean and interval HDI
for i in range(len(rugged_seq)):
        log_gdp_africa = params_post.alpha.sel(africa=0) + params_post.beta.sel(africa=0).values * rugged_seq[i]
        log_gdp_mean_africa.append(np.mean(log_gdp_africa.values))
        log_gdp_hdi_africa.append(az.hdi(log_gdp_africa.values, hdi_prob=0.89))
        
        log_gdp_not_africa = params_post.alpha.sel(africa=1) + params_post.beta.sel(africa=1).values * rugged_seq[i]
        log_gdp_mean_not_africa.append(np.mean(log_gdp_not_africa.values))
        log_gdp_hdi_not_africa.append(az.hdi(log_gdp_not_africa.values, hdi_prob=0.89))
        
log_gdp_hdi_africa = np.array(log_gdp_hdi_africa)
log_gdp_hdi_not_africa = np.array(log_gdp_hdi_not_africa)

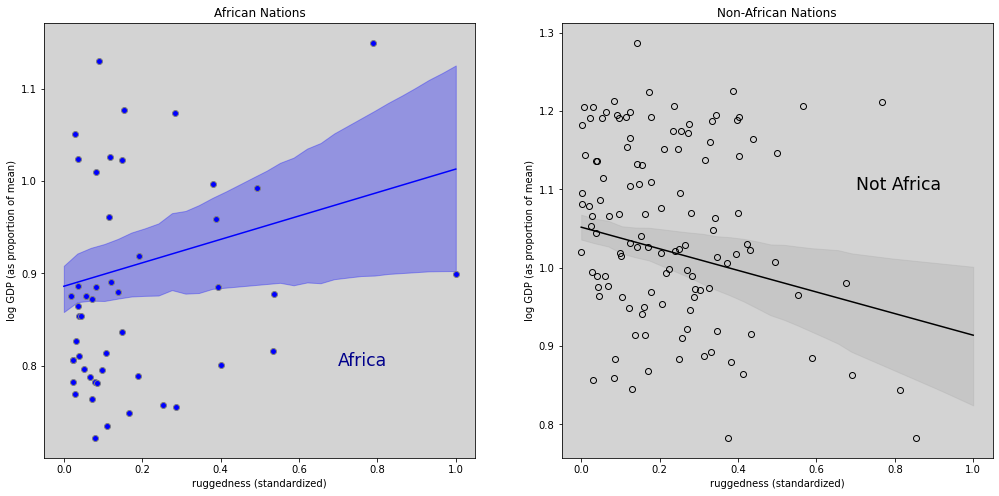
fig = plt.figure(figsize=(17, 8))

gs = GridSpec(1, 2)

# Africa plots
ax_africa = fig.add_subplot(gs[0])

ax_africa.plot(rugged_seq, log_gdp_mean_africa, c='blue')
ax_africa.fill_between(rugged_seq, log_gdp_hdi_africa[:,0], log_gdp_hdi_africa[:,1], color='blue', alpha=0.3)
ax_africa.plot(ddf.loc[ddf.cid == 1,'rugged_std'], ddf.loc[ddf.cid==1, 'log_gdp_std'], 'o', markerfacecolor='blue', color='gray')

ax_africa.set_title('African Nations')
ax_africa.set_xlabel('ruggedness (standardized)')
ax_africa.set_ylabel('log GDP (as proportion of mean)')
ax_africa.text(0.7, 0.8, 'Africa',  fontsize='xx-large', color='darkblue')


# Non africa plots
ax_not_africa = fig.add_subplot(gs[1])

ax_not_africa.plot(rugged_seq, log_gdp_mean_not_africa, c='black')
ax_not_africa.fill_between(rugged_seq, log_gdp_hdi_not_africa[:,0], log_gdp_hdi_not_africa[:,1], color='darkgray', alpha=0.3)
ax_not_africa.plot(ddf.loc[ddf.cid == 2,'rugged_std'], ddf.loc[ddf.cid==2, 'log_gdp_std'], 'o', markerfacecolor='none', color='black')

ax_not_africa.set_title('Non-African Nations')
ax_not_africa.set_xlabel('ruggedness (standardized)')
ax_not_africa.set_ylabel('log GDP (as proportion of mean)')
ax_not_africa.text(0.7, 1.1, 'Not Africa', fontsize='xx-large', color='black')


plt.show()

R Code 8.18¶

log_gdp_delta_mean = []
log_gdp_delta_hdi = []

# Calculation posterior mean and interval HDI
for i in range(len(rugged_seq)):
        log_gdp_africa = params_post.alpha.sel(africa=0) + params_post.beta.sel(africa=0).values * rugged_seq[i]
        log_gdp_not_africa = params_post.alpha.sel(africa=1) + params_post.beta.sel(africa=1).values * rugged_seq[i]
        
        log_gdp_delta = log_gdp_africa - log_gdp_not_africa

        log_gdp_delta_mean.append(np.mean(log_gdp_delta.values))
        log_gdp_delta_hdi.append(az.hdi(log_gdp_delta.values, hdi_prob=0.89))
        
log_gdp_delta_hdi = np.array(log_gdp_delta_hdi)

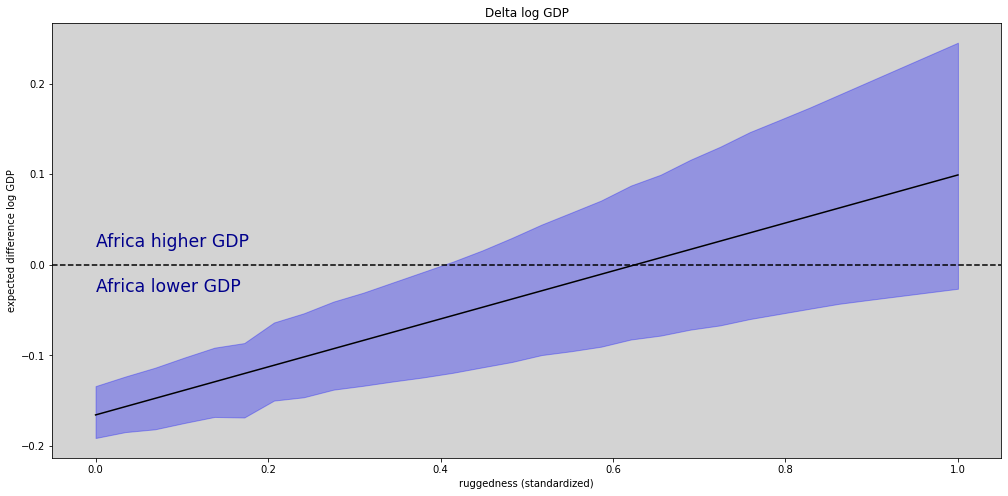
fig = plt.figure(figsize=(17, 8))

gs = GridSpec(1, 1)

# Africa delta log GDP plots
ax_delta = fig.add_subplot(gs[0])

ax_delta.plot(rugged_seq, log_gdp_delta_mean, c='black')
ax_delta.fill_between(rugged_seq, log_gdp_delta_hdi[:,0], log_gdp_delta_hdi[:,1], color='blue', alpha=0.3)

ax_delta.set_title('Delta log GDP')
ax_delta.set_xlabel('ruggedness (standardized)')
ax_delta.set_ylabel('expected difference log GDP')

ax_delta.text(0.0, 0.02, 'Africa higher GDP',  fontsize='xx-large', color='darkblue')
ax_delta.text(0.0, -0.03, 'Africa lower GDP',  fontsize='xx-large', color='darkblue')
ax_delta.axhline(y=0, ls='--', color='black')

plt.show()

R Code 8.19¶

df = pd.read_csv('./data/tulips.csv', sep=';',
                 dtype={
                     'bed': 'category',  # cluster of plants from same section of the greenhouse
                     'water': 'float',  # Predictor: Soil moisture - (1) low and (3) high 
                     'shade': 'float',  # Predictor: Light exposure - (1) high and (3) low
                     'blooms': 'float',  # What we wish to predict
                 })
df.tail()

	bed	water	shade	blooms
22	c	2.0	2.0	135.92
23	c	2.0	3.0	90.66
24	c	3.0	1.0	304.52
25	c	3.0	2.0	249.33
26	c	3.0	3.0	134.59

df.describe(include='category')

	bed
count	27
unique	3
top	a
freq	9

df.describe().T

	count	mean	std	min	25%	50%	75%	max
water	27.0	2.000000	0.832050	1.0	1.000	2.00	3.0	3.00
shade	27.0	2.000000	0.832050	1.0	1.000	2.00	3.0	3.00
blooms	27.0	128.993704	92.683923	0.0	71.115	111.04	190.3	361.66

R Code 8.20¶

df['blooms_std'] = df['blooms'] / df['blooms'].max()
df['water_cent'] = df['water'] - df['water'].mean()
df['shade_cent'] = df['shade'] - df['shade'].mean()

R Code 8.21¶

\[ \alpha \sim Normal(0.5, 1) \]

alpha = np.random.normal(0.5, 1, 1000)

alphas_true = np.any([alpha < 0, alpha > 1], axis=0)  # If (alpha < 0) or (alpha > 1) then True else False

np.sum(alphas_true) / len(alpha)

0.628

R Code 8.22¶

\[ \alpha \sim Normal(0.5, 0.25) \]

alpha = np.random.normal(0.5, 0.25, 1000)

alphas_true = np.any([alpha < 0, alpha > 1], axis=0)  # If (alpha < 0) or (alpha > 1) then True else False

np.sum(alphas_true) / len(alpha)

0.053

R Code 8.23¶

model = """
    data {
        int N;
        vector[N] blooms_std;
        vector[N] water_cent;
        vector[N] shade_cent;
    }
    
    parameters {
        real alpha;
        real beta_w;
        real beta_s;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta_w * water_cent + beta_s * shade_cent;
    }
    
    model {
        // Priori
        
        alpha ~ normal(0.5, 0.25);
        beta_w ~ normal(0, 0.25);
        beta_s ~ normal(0, 0.25);
        sigma ~ exponential(1);
        
        blooms_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] blooms_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(blooms_std[i] | mu[i], sigma);
            blooms_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(df),
    'blooms_std': df.blooms_std.values,   
    'water_cent': df.water_cent.values,
    'shade_cent': df.shade_cent.values,
}

posteriori = stan.build(model, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

az.summary(stan_blooms, var_names=['alpha', 'beta_w', 'beta_s'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	ess_bulk	ess_tail	r_hat
alpha	0.359	0.034	0.298	0.429	0.001	3857.0	2579.0	1.0
beta_w	0.203	0.041	0.126	0.279	0.001	4353.0	3032.0	1.0
beta_s	-0.112	0.041	-0.188	-0.036	0.001	4151.0	2524.0	1.0

R Code 8.24¶

\[ B_i \sim Normal(\mu_i, \sigma) \]

\[ \mu_i = \alpha + \beta_W W_i + \beta_S S_i + \beta_{WS} S_i W_i \]

model = """
    data {
        int N;
        vector[N] blooms_std;
        vector[N] water_cent;
        vector[N] shade_cent;
    }
    
    parameters {
        real alpha;
        real beta_w;
        real beta_s;
        real beta_ws;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta_w * water_cent + beta_s * shade_cent + beta_ws * water_cent .* shade_cent;
    }
    
    model {
        // Priori
        
        alpha ~ normal(0.5, 0.25);
        beta_w ~ normal(0, 0.25);
        beta_s ~ normal(0, 0.25);
        beta_ws ~ normal(0, 0.25);
        sigma ~ exponential(1);
        
        blooms_std ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] blooms_std_hat;
        
        for(i in 1:N){
            log_lik[i] = normal_lpdf(blooms_std[i] | mu[i], sigma);
            blooms_std_hat[i] = normal_rng(mu[i], sigma);
        }
    }
"""

data = {
    'N': len(df),
    'blooms_std': df.blooms_std.values,   
    'water_cent': df.water_cent.values,
    'shade_cent': df.shade_cent.values,
}

posteriori = stan.build(model, data=data)
samples = posteriori.sample(num_chains=4, num_samples=1000)

az.summary(stan_blooms_interaction, var_names=['alpha', 'beta_w', 'beta_s', 'beta_ws'])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	ess_bulk	ess_tail	r_hat
alpha	0.358	0.029	0.301	0.411	0.000	5629.0	2730.0	1.0
beta_w	0.206	0.034	0.145	0.275	0.000	4954.0	2852.0	1.0
beta_s	-0.113	0.034	-0.177	-0.051	0.000	5101.0	3033.0	1.0
beta_ws	-0.143	0.042	-0.220	-0.059	0.001	5011.0	3012.0	1.0

R Code 8.25¶

blooms_post = az.extract(stan_blooms.posterior, num_samples=20)  # get 20 lines
blooms_post_int = az.extract(stan_blooms_interaction.posterior, num_samples=20)  # get 20 lines

# ================
# Plot without interactions

water_seq = np.linspace(-1, 1, 30)

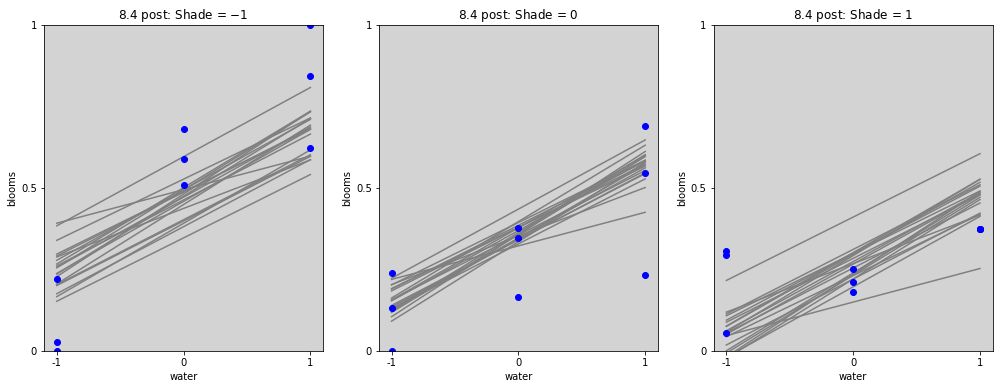
fig = plt.figure(figsize=(17, 6))

gs = GridSpec(1, 3)

shade_cent_values = [-1, 0, 1]

ax = [None] * len(shade_cent_values)

for j, shade_plot_aux in enumerate(shade_cent_values):
    ax[j] = fig.add_subplot(gs[j])

    for i in range(len(blooms_post.alpha)):
        mu = blooms_post.alpha[i].values + \
             blooms_post.beta_w[i].values * water_seq + \
             blooms_post.beta_s[i].values * (shade_plot_aux)

        ax[j].plot(water_seq, mu, c='gray')
        ax[j].set_ylim(0, 1)
        ax[j].set_title(f'8.4 post: Shade = ${shade_plot_aux}$')
        ax[j].set_xlabel('water')
        ax[j].set_ylabel('blooms')
        ax[j].set_xticks(shade_cent_values, shade_cent_values)
        ax[j].set_yticks([0, 0.5, 1.0], [0, 0.5, 1])

    ax[j].plot(
            df.loc[df['shade_cent'] == shade_plot_aux,'water_cent'].values, 
            df.loc[df['shade_cent'] == shade_plot_aux,'blooms_std'].values, 
            'o', c='blue')
    
plt.show()

# ================
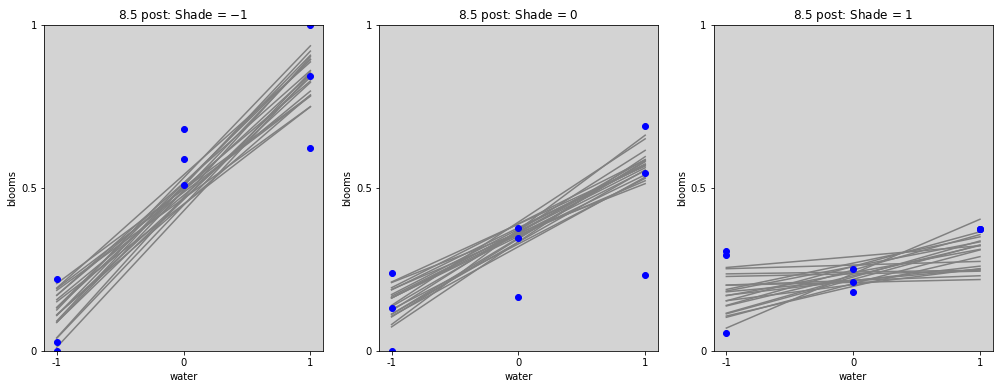
# Plot with interactions

water_seq = np.linspace(-1, 1, 30)

fig = plt.figure(figsize=(17, 6))

gs = GridSpec(1, 3)

shade_cent_values = [-1, 0, 1]

ax = [None] * len(shade_cent_values)

for j, shade_plot_aux in enumerate(shade_cent_values):
    ax[j] = fig.add_subplot(gs[j])

    for i in range(len(blooms_post_int.alpha)):
        mu = blooms_post_int.alpha[i].values + \
             blooms_post_int.beta_w[i].values * water_seq + \
             blooms_post_int.beta_s[i].values * (shade_plot_aux) + \
             blooms_post_int.beta_ws[i].values * water_seq * (shade_plot_aux)

        ax[j].plot(water_seq, mu, c='gray')
        ax[j].set_ylim(0, 1)
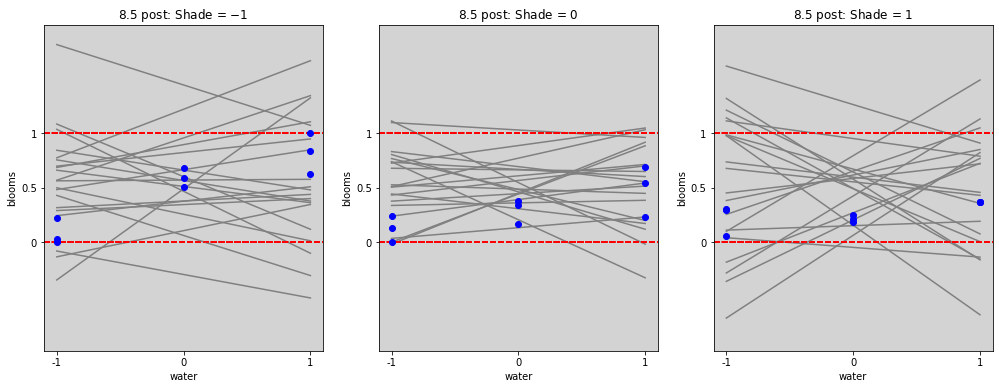
        ax[j].set_title(f'8.5 post: Shade = ${shade_plot_aux}$')
        ax[j].set_xlabel('water')
        ax[j].set_ylabel('blooms')
        ax[j].set_xticks(shade_cent_values, shade_cent_values)
        ax[j].set_yticks([0, 0.5, 1.0], [0, 0.5, 1])

    ax[j].plot(
            df.loc[df['shade_cent'] == shade_plot_aux,'water_cent'].values, 
            df.loc[df['shade_cent'] == shade_plot_aux,'blooms_std'].values, 
            'o', c='blue')
    
plt.show()

R Code 8.26¶

# ================
# Plot without interactions

# Prior
alpha_prior =  np.random.normal(0.5, 0.25, 20)
beta_w_prior =  np.random.normal(0, 0.25, 20)
beta_s_prior =  np.random.normal(0, 0.25, 20)

water_seq = np.linspace(-1, 1, 30)

fig = plt.figure(figsize=(17, 6))

gs = GridSpec(1, 3)

shade_cent_values = [-1, 0, 1]

ax = [None] * len(shade_cent_values)

for j, shade_plot_aux in enumerate(shade_cent_values):
    ax[j] = fig.add_subplot(gs[j])

    for i in range(len(alpha_prior)):
        mu = alpha_prior[i] + \
             beta_w_prior[i] * water_seq + \
             beta_s_prior[i] * (shade_plot_aux)

        ax[j].plot(water_seq, mu, c='gray')
        ax[j].set_ylim(0, 1)
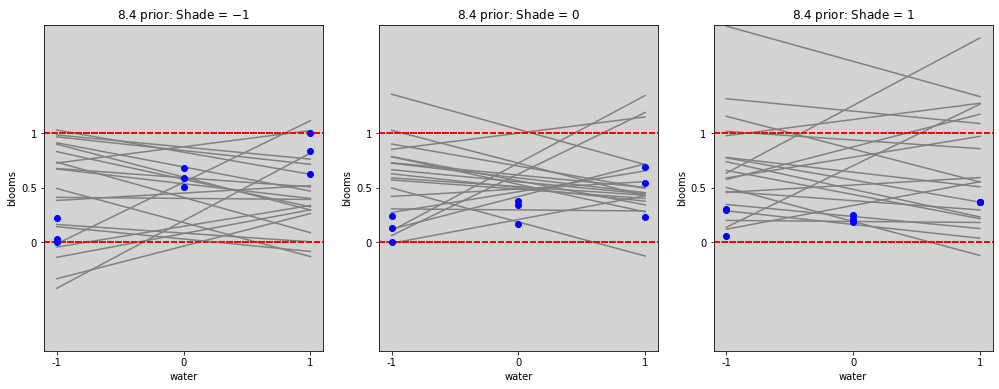
        ax[j].set_title(f'8.4 prior: Shade = ${shade_plot_aux}$')
        ax[j].set_xlabel('water')
        ax[j].set_ylabel('blooms')
        ax[j].set_xticks(shade_cent_values, shade_cent_values)
        ax[j].set_yticks([0, 0.5, 1.0], [0, 0.5, 1])
        ax[j].set_ylim(-1, 2)
        ax[j].axhline(y=1, ls='--', color='red')
        ax[j].axhline(y=0, ls='--', color='red')

    ax[j].plot(
            df.loc[df['shade_cent'] == shade_plot_aux,'water_cent'].values, 
            df.loc[df['shade_cent'] == shade_plot_aux,'blooms_std'].values, 
            'o', c='blue')
    
plt.show()

# ================
# Plot with interactions

# Prior
alpha_prior =  np.random.normal(0.5, 0.25, 20)
beta_w_prior =  np.random.normal(0, 0.25, 20)
beta_s_prior =  np.random.normal(0, 0.25, 20)
beta_ws_prior =  np.random.normal(0, 0.25, 20)

water_seq = np.linspace(-1, 1, 30)

fig = plt.figure(figsize=(17, 6))

gs = GridSpec(1, 3)

shade_cent_values = [-1, 0, 1]

ax = [None] * len(shade_cent_values)

for j, shade_plot_aux in enumerate(shade_cent_values):
    ax[j] = fig.add_subplot(gs[j])

    for i in range(len(alpha_prior)):
        mu = alpha_prior[i] + \
             beta_w_prior[i] * water_seq + \
             beta_s_prior[i] * (shade_plot_aux) + \
             beta_ws_prior[i] * water_seq * (shade_plot_aux)

        ax[j].plot(water_seq, mu, c='gray')
        ax[j].set_ylim(0, 1)
        ax[j].set_title(f'8.5 post: Shade = ${shade_plot_aux}$')
        ax[j].set_xlabel('water')
        ax[j].set_ylabel('blooms')
        ax[j].set_xticks(shade_cent_values, shade_cent_values)
        ax[j].set_yticks([0, 0.5, 1.0], [0, 0.5, 1])
        ax[j].set_ylim(-1, 2)
        ax[j].axhline(y=1, ls='--', color='red')
        ax[j].axhline(y=0, ls='--', color='red')

    ax[j].plot(
            df.loc[df['shade_cent'] == shade_plot_aux,'water_cent'].values, 
            df.loc[df['shade_cent'] == shade_plot_aux,'blooms_std'].values, 
            'o', c='blue')
    
plt.show()

Statistical Rethinking