9 - Markov Chain Monte Carlo¶
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
import pandas as pd
import networkx as nx
# from causalgraphicalmodels import CausalGraphicalModel
import arviz as az
# ArviZ ships with style sheets!
# https://python.arviz.org/en/stable/examples/styles.html#example-styles
az.style.use("arviz-darkgrid")
import xarray as xr
import stan
import nest_asyncio
plt.style.use('default')
plt.rcParams['axes.facecolor'] = 'lightgray'
# To DAG's
import daft
from causalgraphicalmodels import CausalGraphicalModel
# Add fonts to matplotlib to run xkcd
from matplotlib import font_manager
font_dirs = ["fonts/"] # The path to the custom font file.
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)
for font_file in font_files:
font_manager.fontManager.addfont(font_file)
# To make plots like drawing
# plt.xkcd()
# To running the stan in jupyter notebook
nest_asyncio.apply()
R Code 9.1¶
num_weeks = 10000
positions = np.zeros(num_weeks, dtype=int)
current = 10
for i in range(num_weeks):
# Record current position
positions[i] = current
# F/lip coin to generate proposal
proposal = current + np.random.choice([-1, 1], size=1)
# Now make sure he loops around the archipelago
if proposal < 1:
proposal = 10
if proposal > 10:
proposal = 1
# Move?
prob_move = proposal / current
if np.random.uniform(0, 1) < prob_move:
current = proposal
else:
current = current
R Code 8.2¶
plt.figure(figsize=(17, 6))
plt.plot(np.arange(0, 100, dtype=int), positions[0:100], 'o', ms=3)
plt.title('King Markov visits')
plt.xlabel('Island')
plt.ylabel('Week')
plt.show()

R Code 9.3¶
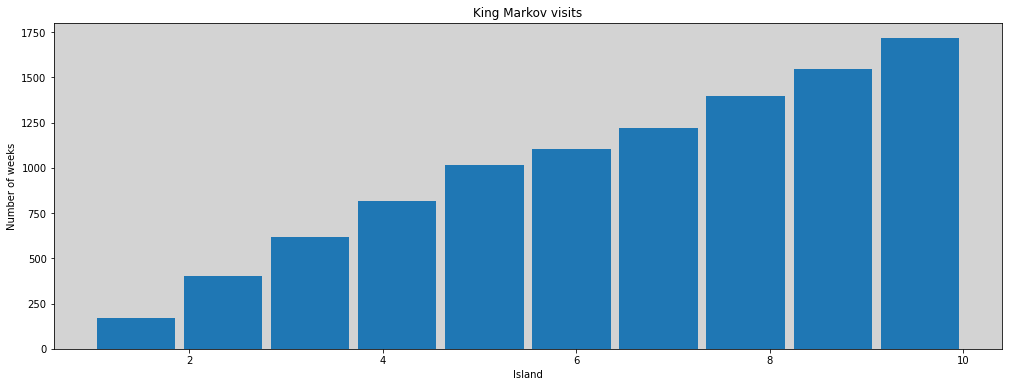
plt.figure(figsize=(17, 6))
plt.hist(positions, rwidth=0.9)
plt.title('King Markov visits')
plt.xlabel('Island')
plt.ylabel('Number of weeks')
plt.show()
R Code 9.4¶
def multivariate_normal(D, T=1000):
""" Return the Gaussian Multivariate standart D-dimensional
Parameter:
===========
D: integer
D is the dimension of the Gaussian Multivariate
T: Integer; default=1000
Qty samples
"""
means = np.repeat(0, D)
diag = np.diag(np.repeat(1, D))
return np.random.multivariate_normal(means, diag, T)
def rad_dist(Y):
""" Return the distance radial from the mode
Parameter:
===========
Y: Multivariate Normal Starndart
"""
return np.sqrt(np.sum(np.power(Y, 2)))
def get_radial_distances(D, T=1000):
""" Return the array of distances of Gaussian Multivariate standart D-dimensional from mode
Parameter:
===========
D: integer
D is the dimension of the Gaussian Multivariate
T: Integer; default=1000
Qty samples
"""
Y = multivariate_normal(D, T)
return [rad_dist(Y[i]) for i in range(T)]
plt.figure(figsize=(17, 6))
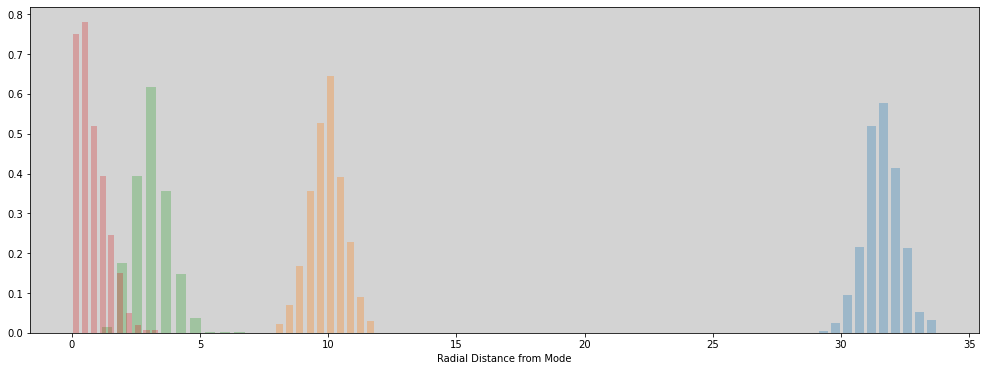
plt.hist(get_radial_distances(1000), alpha=0.3, density=True, rwidth=0.7)
plt.hist(get_radial_distances(100), alpha=0.3, density=True, rwidth=0.7)
plt.hist(get_radial_distances(10), alpha=0.3, density=True, rwidth=0.7)
plt.hist(get_radial_distances(1), alpha=0.3, density=True, rwidth=0.7)
plt.xlabel('Radial Distance from Mode')
plt.show()