.ipynb .pdf

repository open issue

Binder

Contents

7 - Compasso de Ulisses

import numpy as np

from scipy import stats

import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

import pandas as pd
from videpy import Vide

import networkx as nx
# from causalgraphicalmodels import CausalGraphicalModel

import stan
import nest_asyncio

plt.style.use('default')

plt.rcParams['axes.facecolor'] = 'lightgray'

# To DAG's
import daft
from causalgraphicalmodels import CausalGraphicalModel

# To running the stan in jupyter notebook
nest_asyncio.apply()

R Code 7.1 - Pag 194

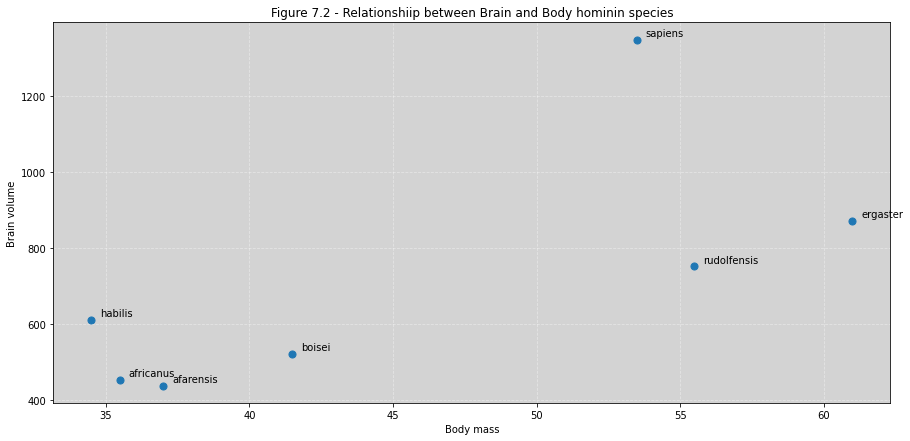
sppnames = ('afarensis', 'africanus', 'habilis',  'boisei', 'rudolfensis', 'ergaster', 'sapiens')
brainvolcc = (438, 452, 612, 521,  752, 871, 1350)
masskg = (37.0, 35.5, 34.5, 41.5, 55.5, 61.0, 53.5)

d = pd.DataFrame({'species':sppnames, 'brain': brainvolcc, 'mass':masskg})
d

	species	brain	mass
0	afarensis	438	37.0
1	africanus	452	35.5
2	habilis	612	34.5
3	boisei	521	41.5
4	rudolfensis	752	55.5
5	ergaster	871	61.0
6	sapiens	1350	53.5

fig, ax = plt.subplots(figsize=(15, 7))
ax.scatter(d.mass, d.brain, marker='o', s=50)

for i, text in enumerate(sppnames):
    ax.annotate(text, (d.mass[i]+0.3, d.brain[i]+10))
    
ax.set_title('Figure 7.2 - Relationshiip between Brain and Body hominin species')
ax.set_xlabel('Body mass')
ax.set_ylabel('Brain volume')

ax.grid(ls='--', color='white', alpha=0.4)
plt.show()

R Code 7.2 - pag 196

np.std(d.mass, ddof=1)

10.90489186863706

d.mass.std()

10.90489186863706

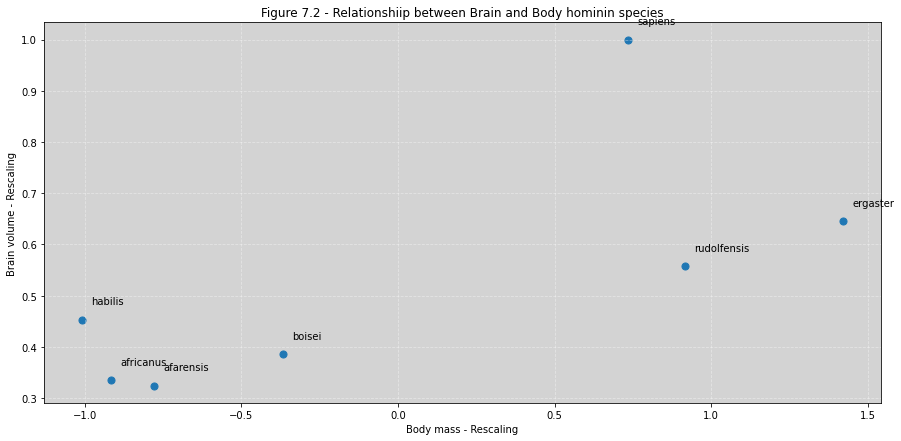
d['mass_std'] = (d.mass - d.mass.mean())/d.mass.std()
d['brain_std'] = d.brain / np.max(d.brain)
d

	species	brain	mass	mass_std	brain_std
0	afarensis	438	37.0	-0.779467	0.324444
1	africanus	452	35.5	-0.917020	0.334815
2	habilis	612	34.5	-1.008722	0.453333
3	boisei	521	41.5	-0.366808	0.385926
4	rudolfensis	752	55.5	0.917020	0.557037
5	ergaster	871	61.0	1.421380	0.645185
6	sapiens	1350	53.5	0.733616	1.000000

fig, ax = plt.subplots(figsize=(15, 7))
ax.scatter(d.mass_std, d.brain_std, marker='o', s=50)

for i, text in enumerate(sppnames):
    ax.annotate(text, (d.mass_std[i]+0.03, d.brain_std[i]+0.03))
    
ax.set_title('Figure 7.2 - Relationshiip between Brain and Body hominin species')
ax.set_xlabel('Body mass - Rescaling')
ax.set_ylabel('Brain volume - Rescaling')

ax.grid(ls='--', color='white', alpha=0.4)
plt.show()

R Code 7.3 - pag 196

Modelo linear:

\(\begin{align} b_i \sim Normal(\mu_i, \sigma) \\ \mu_i = \alpha + \beta m_i \\ \alpha \sim Normal(0.5, 1) \\ \beta \sim Normal(0, 10) \\ \sigma \sim LogNormal(0, 1) \\ \end{align}\)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta;
        real<lower=0> sigma;
        // real log_sigma;  // Like the book
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta * body;
                
        // Prioris
        alpha ~ normal(0.5, 1);
        beta ~ normal(0, 10);
        sigma ~ lognormal(0, 1);
        // log_sigma ~ normal(0, 1);  // Like the book 
        
        // Likelihood
        brain ~ normal(mu, sigma);
        // brain ~ normal(mu, exp(sigma));  // Like the book
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_1 = stan.build(model, data=data)
samples_1 = posteriori_1.sample(num_chains=4, num_samples=1000)

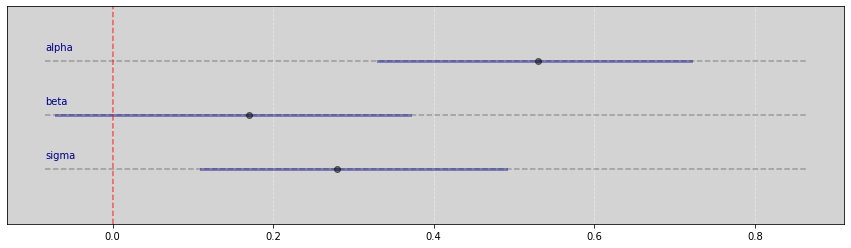
Vide.summary(samples_1)

	mean	std	7.0%	93.0%
alpha	0.53	0.11	0.33	0.72
beta	0.17	0.12	-0.07	0.37
sigma	0.28	0.12	0.11	0.49

Vide.plot_forest(samples_1)

R Code 7.4 - pag 196

Just example code in R

m7.1_OLS <- lm(brain_std ~ brain_std, data=d)

R Code 7.5 - pag 197

def var2(x):
    return np.sum(np.power(x - np.mean(x), 2))/len(x)

mean_std = [np.mean((samples_1['alpha'].flatten() + samples_1['beta'].flatten() * mass)) for mass in d.mass_std.values]
r = mean_std - d.brain_std

resid_var = var2(r)
outcome_var = var2(d.brain_std)

1 - resid_var/outcome_var

0.490158020661996

R Code 7.6 - Pag 197

def R2_is_bad():
    pass

R Code 7.7 - pag 198

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[2];
        real<lower=0> sigma;
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta[1] * body + beta[2] * body^2;
        
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:2){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 1);    
        
        // Likelihood
        brain ~ normal(mu, sigma);
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_2 = stan.build(model, data=data)
samples_2 = posteriori_2.sample(num_chains=4, num_samples=1000)

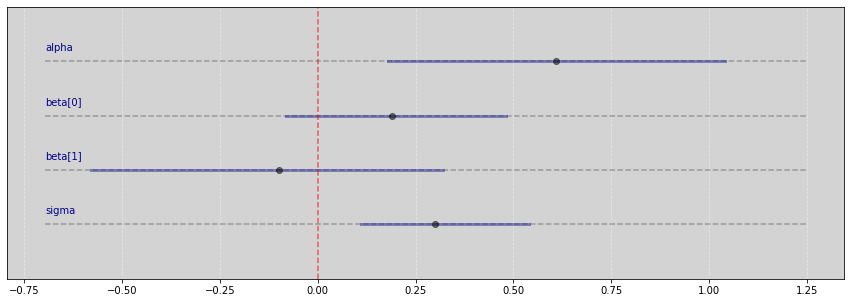
Vide.summary(samples_2)

	mean	std	7.0%	93.0%
alpha	0.61	0.24	0.18	1.04
beta[0]	0.19	0.16	-0.08	0.48
beta[1]	-0.10	0.24	-0.58	0.32
sigma	0.30	0.16	0.11	0.54

Vide.plot_forest(samples_2)

R Code 7.8 - Pag 198

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[3];
        real<lower=0> sigma;
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3;
                     
        // Likelihood
        brain ~ normal(mu, sigma);
        
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:3){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 1);    
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_3 = stan.build(model, data=data)
samples_3 = posteriori_3.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[4];
        real<lower=0> sigma;
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4;
                     
        // Likelihood
        brain ~ normal(mu, sigma);
        
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:4){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 1);    
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_4 = stan.build(model, data=data)
samples_4 = posteriori_4.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[5];
        real<lower=0> sigma;
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4 +
                     beta[5] * body^5;
                     
        // Likelihood
        brain ~ normal(mu, sigma);
        
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:5){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 1);    
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_5 = stan.build(model, data=data)
samples_5 = posteriori_5.sample(num_chains=4, num_samples=1000)

R Code 7.9 - Pag 199

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[6];
    }
    
    model {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4 +
                     beta[5] * body^5 +
                     beta[6] * body^6;
                     
        // Likelihood
        brain ~ normal(mu, 0.001);
        
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:6){
            beta[j] ~ normal(0, 10);
        }    
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_6 = stan.build(model, data=data)
samples_6 = posteriori_6.sample(num_chains=4, num_samples=1000)

R Code 7.10 - Pag 199

mass_seq = np.linspace(start=d.mass_std.min(), stop=d.mass_std.max(), num=100)

pp_1 = [samples_1['alpha'].flatten() + samples_1['beta'].flatten() * mass_i for mass_i in mass_seq]

pp_2 = [samples_2['alpha'].flatten() + 
        samples_2['beta'][0].flatten() * mass_i + 
        samples_2['beta'][1].flatten() * np.power(mass_i, 2) for mass_i in mass_seq]

pp_3 = [samples_3['alpha'].flatten() + 
        samples_3['beta'][0].flatten() * mass_i + 
        samples_3['beta'][1].flatten() * np.power(mass_i, 2) + 
        samples_3['beta'][2].flatten() * np.power(mass_i, 3)
        for mass_i in mass_seq]

pp_4 = [samples_4['alpha'].flatten() + 
        samples_4['beta'][0].flatten() * mass_i + 
        samples_4['beta'][1].flatten() * np.power(mass_i, 2) + 
        samples_4['beta'][2].flatten() * np.power(mass_i, 3) +
        samples_4['beta'][3].flatten() * np.power(mass_i, 4) 
        for mass_i in mass_seq]

pp_5 = [samples_5['alpha'].flatten() + 
        samples_5['beta'][0].flatten() * mass_i + 
        samples_5['beta'][1].flatten() * np.power(mass_i, 2) + 
        samples_5['beta'][2].flatten() * np.power(mass_i, 3) +
        samples_5['beta'][3].flatten() * np.power(mass_i, 4) + 
        samples_5['beta'][4].flatten() * np.power(mass_i, 5) 
        for mass_i in mass_seq]

pp_6 = [samples_6['alpha'].flatten() + 
        samples_6['beta'][0].flatten() * mass_i + 
        samples_6['beta'][1].flatten() * np.power(mass_i, 2) + 
        samples_6['beta'][2].flatten() * np.power(mass_i, 3) +
        samples_6['beta'][3].flatten() * np.power(mass_i, 4) + 
        samples_6['beta'][4].flatten() * np.power(mass_i, 5) + 
        samples_6['beta'][5].flatten() * np.power(mass_i, 6) 
        for mass_i in mass_seq]

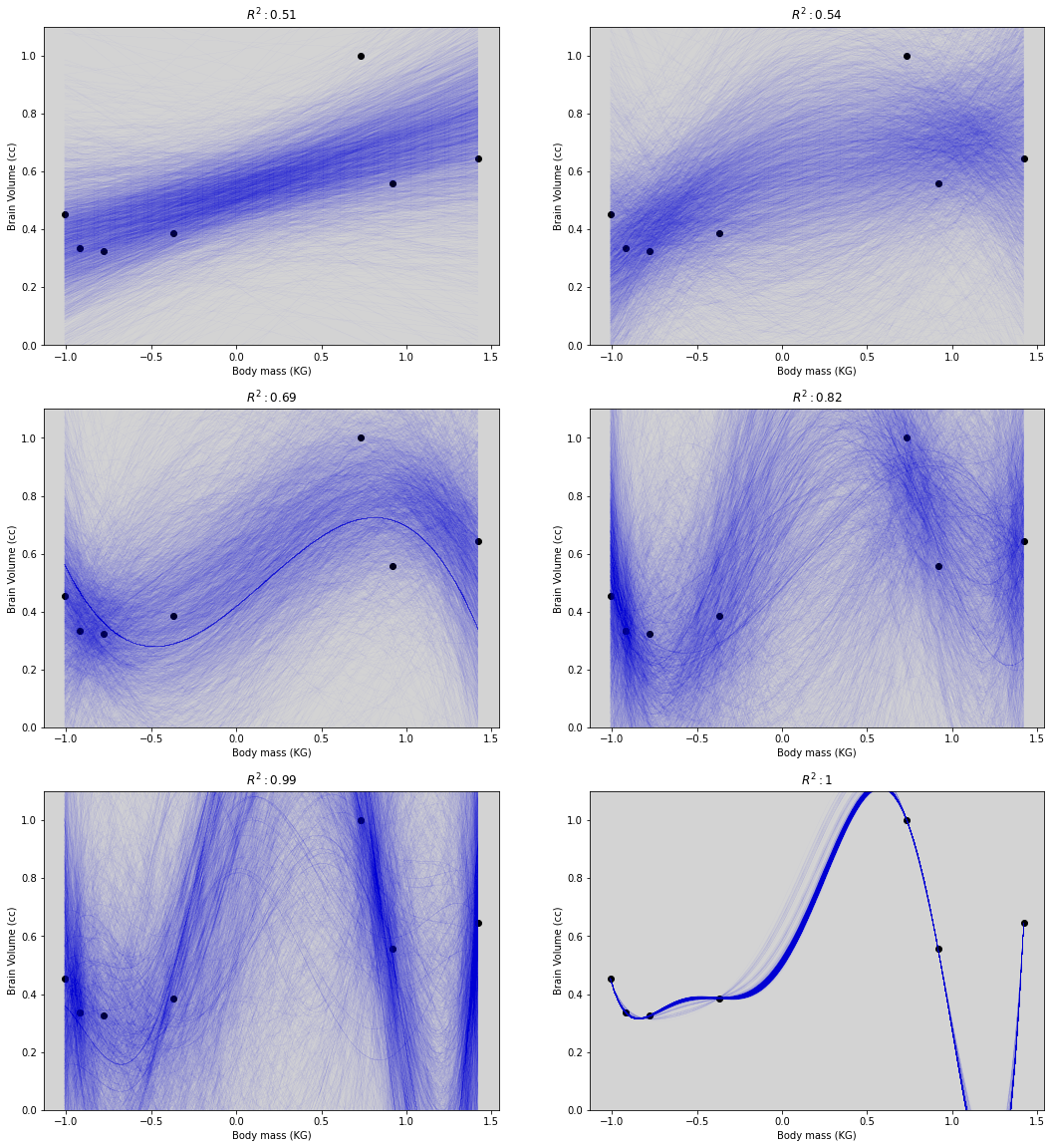
fig = plt.figure(figsize=(18, 20))

gs = GridSpec(nrows=3, ncols=2)

ax1 = fig.add_subplot(gs[0, 0])
ax1.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax1.plot(mass_seq, pp_1, c='blue', lw=0.01)
ax1.set_ylim(0, 1.1)
ax1.set_title('$R^2: 0.51$')
ax1.set_xlabel('Body mass (KG)')
ax1.set_ylabel('Brain Volume (cc)')

ax2 = fig.add_subplot(gs[0, 1])
ax2.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax2.plot(mass_seq, pp_2, c='blue', lw=0.01)
ax2.set_ylim(0, 1.1)
ax2.set_title('$R^2: 0.54$')
ax2.set_xlabel('Body mass (KG)')
ax2.set_ylabel('Brain Volume (cc)')

ax3 = fig.add_subplot(gs[1, 0])
ax3.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax3.plot(mass_seq, pp_3, c='blue', lw=0.01)
ax3.set_ylim(0, 1.1)
ax3.set_title('$R^2: 0.69$')
ax3.set_xlabel('Body mass (KG)')
ax3.set_ylabel('Brain Volume (cc)')

ax4 = fig.add_subplot(gs[1, 1])
ax4.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax4.plot(mass_seq, pp_4, c='blue', lw=0.01)
ax4.set_ylim(0, 1.1)
ax4.set_title('$R^2: 0.82$')
ax4.set_xlabel('Body mass (KG)')
ax4.set_ylabel('Brain Volume (cc)')

ax5 = fig.add_subplot(gs[2, 0])
ax5.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax5.plot(mass_seq, pp_5, c='blue', lw=0.01)
ax5.set_ylim(0, 1.1)
ax5.set_title('$R^2: 0.99$')
ax5.set_xlabel('Body mass (KG)')
ax5.set_ylabel('Brain Volume (cc)')

ax6 = fig.add_subplot(gs[2, 1])
ax6.scatter(d.mass_std.values, d.brain_std.values, c='black')
ax6.plot(mass_seq, pp_6, c='blue', lw=0.01)
ax6.set_ylim(0, 1.1)
ax6.set_title('$R^2: 1$')
ax6.set_xlabel('Body mass (KG)')
ax6.set_ylabel('Brain Volume (cc)')

plt.show()

R Code 7.11 - Pag 201

d.brain_std

0    0.324444
1    0.334815
2    0.453333
3    0.385926
4    0.557037
5    0.645185
6    1.000000
Name: brain_std, dtype: float64

Deletando a linha \(i=3\) do dataframe:

d_deleted_line_3 = d.brain_std.drop(3)
d_deleted_line_3

0    0.324444
1    0.334815
2    0.453333
4    0.557037
5    0.645185
6    1.000000
Name: brain_std, dtype: float64

R Code 7.12 - Pag 206

Entropia da informação: A incerteza contida na distribuição de probabilidade é a média do \(log\) da probabilidade do evento.

def H(p):
    """Information Entropy
    H(p):= -sum(p_i * log(pi))
    """
    if not np.sum(p) == 1:
        print('ProbabilityError: This is not probability, its sum not equal to 1.')
    else:
        return - np.sum([p_i * np.log(p_i) if p_i > 0 else 0 for p_i in p])

p = (0.3, 0.7)  # (p_rain, p_sum)

H(p)

0.6108643020548935

A incerteza do clima de Abu Dhabi é menor, pois é pouco provável que chova.

p_AbuDhabi = (0.01, 0.99)  # (p_rain, p_sum)

H(p_AbuDhabi)

0.056001534354847345

p_3dim = (0.7, 0.15, 0.15)  # (p_1, p_2, p_3)

H(p_3dim)

0.818808456222877

R Code 7.13 - pag 210

References:

• https://stackoverflow.com/questions/49147905/how-to-extract-posterior-samples-of-log-likelihood-from-pystan

• https://mc-stan.org/docs/2_20/functions-reference/normal-distribution.html

Obs:

Here I learned to use the two blocks in stan: transformed parameters and generated quantities.

To calculate the Deviance it is necessary to make these changes.

That’s why I did all 6 estimates again with the calculations needed.

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta;
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        mu = alpha + beta * body;
    }
    
    model {
        // Prioris
        alpha ~ normal(0.5, 1);
        beta ~ normal(0, 10);
        sigma ~ lognormal(0, 1);    
        
        // Likelihood
        brain ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] brain_hat;
        
        for (i in 1:N){
            log_lik[i] = normal_lpdf(brain[i] | mu[i], sigma);
            brain_hat[i] = normal_rng(mu[i], sigma);
        }
        
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_1 = stan.build(model, data=data)
samples_1 = posteriori_1.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[2];
        real<lower=0> sigma;
    }
    
    transformed parameters{
        vector[N] mu;
        mu = alpha + beta[1] * body + 
                     beta[2] * body^2;
    }
    
    model {
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:2){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 10);    
        
        // Likelihood
        brain ~ normal(mu, sigma);
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_2 = stan.build(model, data=data)
samples_2 = posteriori_2.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[3];
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3;
    }
    
    model {                     
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:3){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 10);   
        
        // Likelihood
        brain ~ normal(mu, sigma);
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_3 = stan.build(model, data=data)
samples_3 = posteriori_3.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[4];
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4;
    }
    
    model {
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:4){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 10); 
        
        // Likelihood
        brain ~ normal(mu, sigma);   
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_4 = stan.build(model, data=data)
samples_4 = posteriori_4.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[5];
        real<lower=0> sigma;
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4 +
                     beta[5] * body^5;
    }
    
    model {          
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:5){
            beta[j] ~ normal(0, 10);
        }
        sigma ~ lognormal(0, 10);    
        
        // Likelihood
        brain ~ normal(mu, sigma);
    }
    
    generated quantities {
        vector[N] log_lik;
        vector[N] brain_hat;
        
        for (i in 1:N){
            log_lik[i] = normal_lpdf(brain[i] | mu[i], sigma);
            brain_hat[i] = normal_rng(mu[i], sigma);
        }
        
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_5 = stan.build(model, data=data)
samples_5 = posteriori_5.sample(num_chains=4, num_samples=1000)

model = """
    data {
        int N;
        vector[N] brain;
        vector[N] body;
    }
    
    parameters {
        real alpha;
        real beta[6];
    }
    
    transformed parameters {
        vector[N] mu;
        
        mu = alpha + beta[1] * body   + 
                     beta[2] * body^2 +
                     beta[3] * body^3 +
                     beta[4] * body^4 +
                     beta[5] * body^5 +
                     beta[6] * body^6;
    }
    
    model {          
        // Prioris
        alpha ~ normal(0.5, 1);
        for (j in 1:6){
            beta[j] ~ normal(0, 10);
        }    
        
        // Likelihood
        brain ~ normal(mu, 0.001);
    }
    
    generated quantities {
        vector[N] log_ll_y;
        
        for (i in 1:N){
            log_ll_y[i] = normal_lpdf(brain[i] | mu, 0.001);
        }
    }
"""

data = {
    'N': len(d.brain_std),
    'brain': d.brain_std.values,
    'body': d.mass_std.values,
}

posteriori_6 = stan.build(model, data=data)
samples_6 = posteriori_6.sample(num_chains=4, num_samples=1000)

def lppd(samples, outcome, std_residuals=True):
    """ Calculate the LOG-POINTWISE-PREDICTIVE-DENSITY
    
    samples : stan
        Sampler results of fit posteriori. 
        Need 'mu' already computed.
    
    outcome : list
        List with outcomes the original data.
        
    std_residuals : booleans
        Compute lppd using std of the residuals 
    """
    mu = samples['mu']
    N = len(outcome)
    K = np.shape(mu)[1]  # Qty samples (mu) sampled from posteriori

    outcome = outcome.reshape(-1, 1)

    if std_residuals:
        sigma = (np.sum((mu - outcome)**2, 0) / N)**0.5    
    else:
        sigma = samples['sigma'].flatten()
        
    lppd = np.empty(N, dtype=float)
       
    for i in range(N):
        log_posteriori_predictive = stats.norm.logpdf(outcome[i], mu[i], sigma)

        lppd[i] = np.log(np.sum(np.exp(log_posteriori_predictive))) - np.log(K)
    
    return lppd    

R Code 7.15

Like the book and the this one the values here have slight differeces.

Need review calculations - pag 211 - 2ed

lppd_lm = []

lppd_lm.append(np.sum(lppd(samples_1, d.brain_std.values, std_residuals=True)))
lppd_lm.append(np.sum(lppd(samples_2, d.brain_std.values, std_residuals=True)))
lppd_lm.append(np.sum(lppd(samples_3, d.brain_std.values, std_residuals=True)))
lppd_lm.append(np.sum(lppd(samples_4, d.brain_std.values, std_residuals=True)))
lppd_lm.append(np.sum(lppd(samples_5, d.brain_std.values, std_residuals=True)))
lppd_lm.append(np.sum(lppd(samples_6, d.brain_std.values, std_residuals=True)))

lppd_lm

[1.9566327201814353,
 1.941588551424057,
 2.14378226869432,
 2.754228507821768,
 5.480033073131333,
 40.03033955975213]

import arviz as az
# ArviZ ships with style sheets!
# https://python.arviz.org/en/stable/examples/styles.html#example-styles
az.style.use("arviz-darkgrid")

data = az.from_pystan(
    posterior=samples_5,
    posterior_predictive="brain_hat",
    observed_data=data,
    log_likelihood={"brain": "log_lik"},
)

data

arviz.InferenceData

• posterior

  <xarray.Dataset>
  Dimensions:     (chain: 4, draw: 1000, beta_dim_0: 5, mu_dim_0: 7)
  Coordinates:
    * chain       (chain) int64 0 1 2 3
    * draw        (draw) int64 0 1 2 3 4 5 6 7 ... 992 993 994 995 996 997 998 999
    * beta_dim_0  (beta_dim_0) int64 0 1 2 3 4
    * mu_dim_0    (mu_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      alpha       (chain, draw) float64 0.7899 0.4723 0.1157 ... 0.7226 1.419
      beta        (chain, draw, beta_dim_0) float64 -1.853 -0.7106 ... 0.8986
      sigma       (chain, draw) float64 0.7009 0.3478 0.3989 ... 0.1128 0.1313
      mu          (chain, draw, mu_dim_0) float64 0.7289 0.2776 ... 0.533 1.005
  Attributes:
      created_at:                 2023-08-11T18:53:39.503098
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0
      num_chains:                 4
      num_samples:                1000
      num_thin:                   1
      num_warmup:                 1000
      save_warmup:                0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • beta_dim_0: 5
    • mu_dim_0: 7
  • Coordinates: (4)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • beta_dim_0
      (beta_dim_0)
      int64
      0 1 2 3 4

      array([0, 1, 2, 3, 4])

    • mu_dim_0
      (mu_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (4)
    • alpha
      (chain, draw)
      float64
      0.7899 0.4723 ... 0.7226 1.419

      array([[ 0.78987293,  0.47233452,  0.11573143, ...,  0.7792361 ,
               0.7792361 ,  0.7792361 ],
             [ 1.01331428,  1.02187202,  0.8845154 , ...,  1.09216952,
               0.72849058,  0.75621562],
             [-0.77690797,  0.78264016,  0.0248647 , ...,  0.71938448,
               0.68199666,  0.59996863],
             [ 1.02186661,  1.14724822,  1.26341696, ...,  1.26102784,
               0.72261203,  1.41932641]])

    • beta
      (chain, draw, beta_dim_0)
      float64
      -1.853 -0.7106 ... 0.9055 0.8986

      array([[[-1.85264604, -0.7105659 ,  2.77220961,  0.126569  ,
               -0.67016469],
              [-0.98779445, -0.01819979,  4.01543514,  0.77923001,
               -2.23508551],
              [-1.28918168, -0.72377396,  3.13577297,  1.24513507,
               -1.77637242],
              ...,
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271],
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271],
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271]],
      
             [[ 1.8700364 , -0.58236774, -3.27650175, -0.0797799 ,
                1.35473859],
              [ 1.82111435, -0.5074553 , -3.21928236, -0.16178733,
                1.37306453],
              [ 2.0044353 , -0.33640789, -3.53766117, -0.19579082,
                1.46457748],
      ...
              [-0.75352365,  0.05556392,  1.23676844, -0.39631079,
               -0.25550218],
              [-0.13320207,  0.20417305,  0.68549199, -0.14222021,
               -0.27238981],
              [ 0.06648903,  0.01576798,  0.63453191, -0.06929369,
               -0.30563343]],
      
             [[ 1.62438068,  0.35683278, -3.27142503, -1.04963209,
                1.80991864],
              [ 1.34328151,  0.0511817 , -3.36710357, -1.12610104,
                1.9829131 ],
              [ 1.46399565, -0.28358385, -2.92408998, -0.70225059,
                1.53345295],
              ...,
              [ 1.45964569, -1.62303603, -2.10083532,  0.78522526,
                0.60857052],
              [ 0.98134573,  0.11795768, -1.61655869, -0.2982359 ,
                0.72860781],
              [ 1.87211942, -2.03014332, -2.9094564 ,  0.90545583,
                0.89859179]]])

    • sigma
      (chain, draw)
      float64
      0.7009 0.3478 ... 0.1128 0.1313

      array([[0.70090975, 0.34781307, 0.3988521 , ..., 0.09006732, 0.09006732,
              0.09006732],
             [0.04488868, 0.04896691, 0.04814223, ..., 0.04552586, 0.04958059,
              0.04446534],
             [0.56074654, 1.42463415, 0.67589924, ..., 0.28199782, 0.25907059,
              0.23322822],
             [0.21959001, 0.23356949, 0.27390146, ..., 0.12010018, 0.11277224,
              0.13131567]])

    • mu
      (chain, draw, mu_dim_0)
      float64
      0.7289 0.2776 ... 0.533 1.005

      array([[[ 7.28919717e-01,  2.77567058e-01, -7.87697729e-02, ...,
                2.86121279e-01,  1.31034710e+00,  3.71185270e-02],
              [ 2.60352419e-01,  2.66808219e-01,  4.69848718e-01, ...,
                1.74932412e+00,  7.75841089e-01,  1.07404277e+00],
              [ 1.66573415e-01,  3.03598139e-01,  6.05509856e-01, ...,
                4.71592155e-01,  6.02265414e-01,  1.71197116e-03],
              ...,
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00],
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00],
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00]],
      
             [[ 3.34287096e-01,  4.00452975e-01,  3.99923091e-01, ...,
                5.33886880e-01,  6.19905523e-01,  1.04289140e+00],
              [ 3.63849334e-01,  4.02868641e-01,  3.71279614e-01, ...,
                5.58594290e-01,  6.46178378e-01,  1.05860877e+00],
              [ 2.99417529e-01,  4.03367719e-01,  4.19049991e-01, ...,
                5.22966599e-01,  5.92824205e-01,  1.03168802e+00],
      ...
              [ 6.82004262e-01,  3.88811698e-01,  1.23127713e-01, ...,
                5.82901220e-01,  2.12202291e-01,  5.15716322e-01],
              [ 6.11113652e-01,  5.23292485e-01,  4.57755981e-01, ...,
                9.82945842e-01,  7.12840550e-01,  8.65737066e-01],
              [ 3.19583035e-01,  2.12134858e-01,  1.45117502e-01, ...,
                9.16319042e-01,  4.92467674e-01,  8.22746303e-01]],
      
             [[ 6.13563851e-01,  4.39150199e-01,  1.27206687e-01, ...,
                7.20217332e-01,  8.73502172e-01,  1.19450541e+00],
              [ 7.39656662e-01,  4.72799666e-01,  6.34941484e-02, ...,
                3.15121018e-01,  3.98596403e-01,  9.26003605e-01],
              [ 6.34321562e-01,  4.46322393e-01,  1.70795934e-01, ...,
                6.10366151e-01,  4.04610087e-01,  1.15273707e+00],
              ...,
              [ 2.46841834e-01,  3.38333776e-01,  4.70868706e-01, ...,
                5.64570460e-01,  7.59597168e-01,  9.85634704e-01],
              [ 4.75187567e-01,  4.85110184e-01,  4.42240000e-01, ...,
                7.36703062e-01,  7.23423521e-01,  9.36206274e-01],
              [ 1.80165051e-01,  2.96553153e-01,  4.50409276e-01, ...,
                4.08298078e-01,  5.32963684e-01,  1.00461600e+00]]])

  • Indexes: (4)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • beta_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4], dtype='int64', name='beta_dim_0'))

    • mu_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='mu_dim_0'))

  • Attributes: (9)

    created_at :

    2023-08-11T18:53:39.503098

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

    num_chains :

    4

    num_samples :

    1000

    num_thin :

    1

    num_warmup :

    1000

    save_warmup :

    0

  
  
• posterior_predictive

  <xarray.Dataset>
  Dimensions:          (chain: 4, draw: 1000, brain_hat_dim_0: 7)
  Coordinates:
    * chain            (chain) int64 0 1 2 3
    * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
    * brain_hat_dim_0  (brain_hat_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      brain_hat        (chain, draw, brain_hat_dim_0) float64 -0.6716 ... 1.096
  Attributes:
      created_at:                 2023-08-11T18:53:39.659568
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • brain_hat_dim_0: 7
  • Coordinates: (3)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • brain_hat_dim_0
      (brain_hat_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (1)
    • brain_hat
      (chain, draw, brain_hat_dim_0)
      float64
      -0.6716 0.7404 ... 0.5696 1.096

      array([[[-0.67157625,  0.74044835, -0.05370771, ...,  0.41218331,
                0.31817051, -0.56809302],
              [ 0.14376081,  0.76836261,  0.67444754, ...,  1.63616778,
                0.33656255,  1.07186457],
              [ 0.0949888 ,  0.13368191,  0.27441397, ...,  1.14491828,
                0.34147127, -0.17442567],
              ...,
              [ 0.33247667,  0.46912963,  0.50955097, ...,  0.65775759,
                0.69695317,  0.8870647 ],
              [ 0.38427196,  0.40753803,  0.57867721, ...,  0.64500619,
                0.69391179,  1.12743   ],
              [ 0.27838681,  0.41336347,  0.69728829, ...,  0.64036479,
                0.66338501,  1.01368887]],
      
             [[ 0.38461929,  0.43157113,  0.39087932, ...,  0.52886506,
                0.61978389,  1.08284428],
              [ 0.27913648,  0.4830043 ,  0.39271807, ...,  0.49234028,
                0.71803543,  1.00321182],
              [ 0.30125609,  0.39467348,  0.4280089 , ...,  0.33363188,
                0.67734479,  1.05794528],
      ...
              [ 0.90842314,  0.48742629,  0.50223053, ...,  1.11775084,
                0.45654165,  0.62486554],
              [ 0.6143996 ,  0.24072102,  0.4114903 , ...,  1.51608438,
                0.54100887,  0.80509306],
              [ 0.46456858,  0.0884946 ,  0.57334588, ...,  0.41437296,
                0.90743546,  0.78007579]],
      
             [[ 0.63935769,  0.06836551, -0.015311  , ...,  1.15595971,
                1.05760951,  1.2312529 ],
              [ 0.35213352,  0.197653  ,  0.29754935, ...,  0.47394989,
                0.62338563,  0.65766756],
              [ 1.1548429 ,  0.25337811,  0.02290543, ...,  0.4648817 ,
                0.05834947,  1.08793272],
              ...,
              [ 0.34564091,  0.37021532,  0.44659541, ...,  0.42250087,
                0.67991483,  1.07335426],
              [ 0.27292318,  0.6111944 ,  0.6369111 , ...,  0.76217779,
                1.02446786,  0.83080833],
              [ 0.28299893,  0.3752658 ,  0.63134444, ...,  0.64706566,
                0.56957333,  1.0960166 ]]])

  • Indexes: (3)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • brain_hat_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='brain_hat_dim_0'))

  • Attributes: (4)

    created_at :

    2023-08-11T18:53:39.659568

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

  
  
• log_likelihood

  <xarray.Dataset>
  Dimensions:      (chain: 4, draw: 1000, brain_dim_0: 7)
  Coordinates:
    * chain        (chain) int64 0 1 2 3
    * draw         (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
    * brain_dim_0  (brain_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      brain        (chain, draw, brain_dim_0) float64 -0.7301 -0.5669 ... 1.111
  Attributes:
      created_at:                 2023-08-11T18:53:39.614761
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • brain_dim_0: 7
  • Coordinates: (3)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • brain_dim_0
      (brain_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (1)
    • brain
      (chain, draw, brain_dim_0)
      float64
      -0.7301 -0.5669 ... 0.746 1.111

      array([[[-7.30068341e-01, -5.66897907e-01, -8.51724842e-01, ...,
               -6.38261315e-01, -1.01386095e+00, -1.50717005e+00],
              [ 1.20173589e-01,  1.18036313e-01,  1.36024235e-01, ...,
               -5.73828167e+00,  6.65951965e-02,  1.14492434e-01],
              [-7.81080838e-02, -2.83674445e-03, -7.25588796e-02, ...,
               -2.27205375e-02, -5.56370418e-03, -3.13203502e+00],
              ...,
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01],
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01],
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01]],
      
             [[ 2.16059186e+00,  1.11555375e+00,  1.47677427e+00, ...,
                2.05164561e+00,  2.02605458e+00,  1.72813531e+00],
              [ 1.77388096e+00,  1.13191083e+00,  6.93691124e-01, ...,
                2.09716635e+00,  2.09746634e+00,  1.38138042e+00],
              [ 1.97953314e+00,  1.10081715e+00,  1.86109520e+00, ...,
                1.86423472e+00,  1.52318641e+00,  1.89803239e+00],
      ...
              [-4.56934270e-01,  3.28585167e-01, -3.38645684e-01, ...,
                3.42711356e-01, -8.31827936e-01, -1.12769600e+00],
              [-1.80487408e-01,  1.67077330e-01,  4.31570453e-01, ...,
               -9.19631222e-01,  3.97617432e-01,  2.97425436e-01],
              [ 5.36582065e-01,  3.98456983e-01, -3.36408697e-01, ...,
               -6.49730780e-01,  3.22418695e-01,  2.47998479e-01]],
      
             [[-2.69706428e-01,  4.84176855e-01, -5.05797947e-01, ...,
                3.20945718e-01,  5.65226674e-02,  2.04763636e-01],
              [-1.04473911e+00,  3.60835046e-01, -8.57527069e-01, ...,
               -1.03604572e-03, -2.19569449e-02,  4.85153863e-01],
              [-2.63922705e-01,  2.93179724e-01, -1.55978078e-01, ...,
                3.57093938e-01, -9.68098218e-03,  2.20569887e-01],
              ...,
              [ 9.91736278e-01,  1.20006130e+00,  1.18983165e+00, ...,
                1.19852327e+00,  7.46731041e-01,  1.19333716e+00],
              [ 3.70057543e-01,  3.75356947e-01,  1.25860825e+00, ...,
               -5.65829205e-03,  1.02278603e+00,  1.10344595e+00],
              [ 5.07617798e-01,  1.06876389e+00,  1.11096469e+00, ...,
                4.69727833e-01,  7.46047704e-01,  1.11059478e+00]]])

  • Indexes: (3)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • brain_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='brain_dim_0'))

  • Attributes: (4)

    created_at :

    2023-08-11T18:53:39.614761

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

  
  
• sample_stats

  <xarray.Dataset>
  Dimensions:          (chain: 4, draw: 1000)
  Coordinates:
    * chain            (chain) int64 0 1 2 3
    * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
  Data variables:
      acceptance_rate  (chain, draw) float64 0.9942 0.9932 1.0 ... 0.7437 0.6009
      step_size        (chain, draw) float64 0.02283 0.02283 ... 0.01823 0.01823
      tree_depth       (chain, draw) int64 6 7 5 4 8 6 5 4 5 ... 5 6 7 7 5 7 8 7 7
      n_steps          (chain, draw) int64 63 159 31 31 255 ... 47 127 255 255 191
      diverging        (chain, draw) bool False False False ... False False False
      energy           (chain, draw) float64 2.459 5.23 0.8842 ... -7.189 -5.73
      lp               (chain, draw) float64 -1.21 0.03107 2.038 ... 10.68 9.605
  Attributes:
      created_at:                 2023-08-11T18:53:39.561999
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0
      num_chains:                 4
      num_samples:                1000
      num_thin:                   1
      num_warmup:                 1000
      save_warmup:                0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

  • Data variables: (7)
    • acceptance_rate
      (chain, draw)
      float64
      0.9942 0.9932 1.0 ... 0.7437 0.6009

      array([[9.94233707e-01, 9.93165704e-01, 1.00000000e+00, ...,
              2.58318986e-01, 1.48519049e-04, 6.71099767e-02],
             [7.70774184e-01, 1.80592293e-02, 2.50854737e-01, ...,
              2.98825241e-01, 8.26983265e-01, 4.41928941e-01],
             [9.85851276e-01, 9.91385247e-01, 9.79344898e-01, ...,
              8.60362083e-01, 6.29604725e-01, 6.21876881e-01],
             [9.95387414e-01, 9.99909983e-01, 9.99330539e-01, ...,
              9.87221552e-01, 7.43663516e-01, 6.00850499e-01]])

    • step_size
      (chain, draw)
      float64
      0.02283 0.02283 ... 0.01823 0.01823

      array([[0.02283011, 0.02283011, 0.02283011, ..., 0.02283011, 0.02283011,
              0.02283011],
             [0.00923471, 0.00923471, 0.00923471, ..., 0.00923471, 0.00923471,
              0.00923471],
             [0.02833399, 0.02833399, 0.02833399, ..., 0.02833399, 0.02833399,
              0.02833399],
             [0.01823457, 0.01823457, 0.01823457, ..., 0.01823457, 0.01823457,
              0.01823457]])

    • tree_depth
      (chain, draw)
      int64
      6 7 5 4 8 6 5 4 ... 6 7 7 5 7 8 7 7

      array([[6, 7, 5, ..., 1, 1, 1],
             [3, 6, 6, ..., 4, 7, 4],
             [8, 8, 7, ..., 6, 6, 5],
             [6, 5, 6, ..., 8, 7, 7]])

    • n_steps
      (chain, draw)
      int64
      63 159 31 31 ... 127 255 255 191

      array([[ 63, 159,  31, ...,   3,   2,   3],
             [ 15,  63,  63, ...,  15, 127,  17],
             [255, 511, 223, ...,  63,  63,  63],
             [ 63,  31, 127, ..., 255, 255, 191]])

    • diverging
      (chain, draw)
      bool
      False False False ... False False

      array([[False, False, False, ...,  True,  True,  True],
             [False, False, False, ..., False, False,  True],
             [False, False, False, ..., False, False, False],
             [False, False, False, ..., False, False, False]])

    • energy
      (chain, draw)
      float64
      2.459 5.23 0.8842 ... -7.189 -5.73

      array([[  2.45889561,   5.23014587,   0.8842482 , ...,  -5.24178702,
               -7.52119165,  -8.22620056],
             [-12.63637198, -12.02113756, -11.70029831, ..., -13.51513333,
              -13.30583019,  -3.70330084],
             [  3.81284024,  12.21204895,  12.16631997, ...,   0.12223333,
                1.31505589,  -4.03915439],
             [ -2.14973909,  -2.49191708,  -0.2733382 , ...,  -6.040826  ,
               -7.18920473,  -5.72972827]])

    • lp
      (chain, draw)
      float64
      -1.21 0.03107 2.038 ... 10.68 9.605

      array([[-1.2099401 ,  0.0310734 ,  2.03763653, ..., 10.35927788,
              10.35927788, 10.35927788],
             [17.94392058, 16.07488155, 14.50387307, ..., 16.51494071,
              14.95817912, 13.73149783],
             [-0.84080971, -7.14573667, -4.55199362, ...,  1.82542767,
               5.26002971,  6.31266796],
             [ 5.66941622,  3.1314764 ,  4.76632921, ..., 10.95431518,
              10.68023411,  9.60531483]])

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

  • Attributes: (9)

    created_at :

    2023-08-11T18:53:39.561999

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

    num_chains :

    4

    num_samples :

    1000

    num_thin :

    1

    num_warmup :

    1000

    save_warmup :

    0

  
  

data5 = az.from_pystan(
    posterior=samples_5,
    posterior_predictive="brain_hat",
    observed_data=data,
    log_likelihood={"brain": "log_lik"},
)

data5

arviz.InferenceData

• posterior

  <xarray.Dataset>
  Dimensions:     (chain: 4, draw: 1000, beta_dim_0: 5, mu_dim_0: 7)
  Coordinates:
    * chain       (chain) int64 0 1 2 3
    * draw        (draw) int64 0 1 2 3 4 5 6 7 ... 992 993 994 995 996 997 998 999
    * beta_dim_0  (beta_dim_0) int64 0 1 2 3 4
    * mu_dim_0    (mu_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      alpha       (chain, draw) float64 0.7899 0.4723 0.1157 ... 0.7226 1.419
      beta        (chain, draw, beta_dim_0) float64 -1.853 -0.7106 ... 0.8986
      sigma       (chain, draw) float64 0.7009 0.3478 0.3989 ... 0.1128 0.1313
      mu          (chain, draw, mu_dim_0) float64 0.7289 0.2776 ... 0.533 1.005
  Attributes:
      created_at:                 2023-08-11T18:53:39.756266
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0
      num_chains:                 4
      num_samples:                1000
      num_thin:                   1
      num_warmup:                 1000
      save_warmup:                0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • beta_dim_0: 5
    • mu_dim_0: 7
  • Coordinates: (4)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • beta_dim_0
      (beta_dim_0)
      int64
      0 1 2 3 4

      array([0, 1, 2, 3, 4])

    • mu_dim_0
      (mu_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (4)
    • alpha
      (chain, draw)
      float64
      0.7899 0.4723 ... 0.7226 1.419

      array([[ 0.78987293,  0.47233452,  0.11573143, ...,  0.7792361 ,
               0.7792361 ,  0.7792361 ],
             [ 1.01331428,  1.02187202,  0.8845154 , ...,  1.09216952,
               0.72849058,  0.75621562],
             [-0.77690797,  0.78264016,  0.0248647 , ...,  0.71938448,
               0.68199666,  0.59996863],
             [ 1.02186661,  1.14724822,  1.26341696, ...,  1.26102784,
               0.72261203,  1.41932641]])

    • beta
      (chain, draw, beta_dim_0)
      float64
      -1.853 -0.7106 ... 0.9055 0.8986

      array([[[-1.85264604, -0.7105659 ,  2.77220961,  0.126569  ,
               -0.67016469],
              [-0.98779445, -0.01819979,  4.01543514,  0.77923001,
               -2.23508551],
              [-1.28918168, -0.72377396,  3.13577297,  1.24513507,
               -1.77637242],
              ...,
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271],
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271],
              [ 1.98218068,  0.07544162, -3.49192098, -0.36988237,
                1.45923271]],
      
             [[ 1.8700364 , -0.58236774, -3.27650175, -0.0797799 ,
                1.35473859],
              [ 1.82111435, -0.5074553 , -3.21928236, -0.16178733,
                1.37306453],
              [ 2.0044353 , -0.33640789, -3.53766117, -0.19579082,
                1.46457748],
      ...
              [-0.75352365,  0.05556392,  1.23676844, -0.39631079,
               -0.25550218],
              [-0.13320207,  0.20417305,  0.68549199, -0.14222021,
               -0.27238981],
              [ 0.06648903,  0.01576798,  0.63453191, -0.06929369,
               -0.30563343]],
      
             [[ 1.62438068,  0.35683278, -3.27142503, -1.04963209,
                1.80991864],
              [ 1.34328151,  0.0511817 , -3.36710357, -1.12610104,
                1.9829131 ],
              [ 1.46399565, -0.28358385, -2.92408998, -0.70225059,
                1.53345295],
              ...,
              [ 1.45964569, -1.62303603, -2.10083532,  0.78522526,
                0.60857052],
              [ 0.98134573,  0.11795768, -1.61655869, -0.2982359 ,
                0.72860781],
              [ 1.87211942, -2.03014332, -2.9094564 ,  0.90545583,
                0.89859179]]])

    • sigma
      (chain, draw)
      float64
      0.7009 0.3478 ... 0.1128 0.1313

      array([[0.70090975, 0.34781307, 0.3988521 , ..., 0.09006732, 0.09006732,
              0.09006732],
             [0.04488868, 0.04896691, 0.04814223, ..., 0.04552586, 0.04958059,
              0.04446534],
             [0.56074654, 1.42463415, 0.67589924, ..., 0.28199782, 0.25907059,
              0.23322822],
             [0.21959001, 0.23356949, 0.27390146, ..., 0.12010018, 0.11277224,
              0.13131567]])

    • mu
      (chain, draw, mu_dim_0)
      float64
      0.7289 0.2776 ... 0.533 1.005

      array([[[ 7.28919717e-01,  2.77567058e-01, -7.87697729e-02, ...,
                2.86121279e-01,  1.31034710e+00,  3.71185270e-02],
              [ 2.60352419e-01,  2.66808219e-01,  4.69848718e-01, ...,
                1.74932412e+00,  7.75841089e-01,  1.07404277e+00],
              [ 1.66573415e-01,  3.03598139e-01,  6.05509856e-01, ...,
                4.71592155e-01,  6.02265414e-01,  1.71197116e-03],
              ...,
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00],
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00],
              [ 3.77323899e-01,  5.09914842e-01,  5.33673820e-01, ...,
                6.52310593e-01,  6.77732648e-01,  1.09823446e+00]],
      
             [[ 3.34287096e-01,  4.00452975e-01,  3.99923091e-01, ...,
                5.33886880e-01,  6.19905523e-01,  1.04289140e+00],
              [ 3.63849334e-01,  4.02868641e-01,  3.71279614e-01, ...,
                5.58594290e-01,  6.46178378e-01,  1.05860877e+00],
              [ 2.99417529e-01,  4.03367719e-01,  4.19049991e-01, ...,
                5.22966599e-01,  5.92824205e-01,  1.03168802e+00],
      ...
              [ 6.82004262e-01,  3.88811698e-01,  1.23127713e-01, ...,
                5.82901220e-01,  2.12202291e-01,  5.15716322e-01],
              [ 6.11113652e-01,  5.23292485e-01,  4.57755981e-01, ...,
                9.82945842e-01,  7.12840550e-01,  8.65737066e-01],
              [ 3.19583035e-01,  2.12134858e-01,  1.45117502e-01, ...,
                9.16319042e-01,  4.92467674e-01,  8.22746303e-01]],
      
             [[ 6.13563851e-01,  4.39150199e-01,  1.27206687e-01, ...,
                7.20217332e-01,  8.73502172e-01,  1.19450541e+00],
              [ 7.39656662e-01,  4.72799666e-01,  6.34941484e-02, ...,
                3.15121018e-01,  3.98596403e-01,  9.26003605e-01],
              [ 6.34321562e-01,  4.46322393e-01,  1.70795934e-01, ...,
                6.10366151e-01,  4.04610087e-01,  1.15273707e+00],
              ...,
              [ 2.46841834e-01,  3.38333776e-01,  4.70868706e-01, ...,
                5.64570460e-01,  7.59597168e-01,  9.85634704e-01],
              [ 4.75187567e-01,  4.85110184e-01,  4.42240000e-01, ...,
                7.36703062e-01,  7.23423521e-01,  9.36206274e-01],
              [ 1.80165051e-01,  2.96553153e-01,  4.50409276e-01, ...,
                4.08298078e-01,  5.32963684e-01,  1.00461600e+00]]])

  • Indexes: (4)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • beta_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4], dtype='int64', name='beta_dim_0'))

    • mu_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='mu_dim_0'))

  • Attributes: (9)

    created_at :

    2023-08-11T18:53:39.756266

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

    num_chains :

    4

    num_samples :

    1000

    num_thin :

    1

    num_warmup :

    1000

    save_warmup :

    0

  
  
• posterior_predictive

  <xarray.Dataset>
  Dimensions:          (chain: 4, draw: 1000, brain_hat_dim_0: 7)
  Coordinates:
    * chain            (chain) int64 0 1 2 3
    * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
    * brain_hat_dim_0  (brain_hat_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      brain_hat        (chain, draw, brain_hat_dim_0) float64 -0.6716 ... 1.096
  Attributes:
      created_at:                 2023-08-11T18:53:39.902129
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • brain_hat_dim_0: 7
  • Coordinates: (3)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • brain_hat_dim_0
      (brain_hat_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (1)
    • brain_hat
      (chain, draw, brain_hat_dim_0)
      float64
      -0.6716 0.7404 ... 0.5696 1.096

      array([[[-0.67157625,  0.74044835, -0.05370771, ...,  0.41218331,
                0.31817051, -0.56809302],
              [ 0.14376081,  0.76836261,  0.67444754, ...,  1.63616778,
                0.33656255,  1.07186457],
              [ 0.0949888 ,  0.13368191,  0.27441397, ...,  1.14491828,
                0.34147127, -0.17442567],
              ...,
              [ 0.33247667,  0.46912963,  0.50955097, ...,  0.65775759,
                0.69695317,  0.8870647 ],
              [ 0.38427196,  0.40753803,  0.57867721, ...,  0.64500619,
                0.69391179,  1.12743   ],
              [ 0.27838681,  0.41336347,  0.69728829, ...,  0.64036479,
                0.66338501,  1.01368887]],
      
             [[ 0.38461929,  0.43157113,  0.39087932, ...,  0.52886506,
                0.61978389,  1.08284428],
              [ 0.27913648,  0.4830043 ,  0.39271807, ...,  0.49234028,
                0.71803543,  1.00321182],
              [ 0.30125609,  0.39467348,  0.4280089 , ...,  0.33363188,
                0.67734479,  1.05794528],
      ...
              [ 0.90842314,  0.48742629,  0.50223053, ...,  1.11775084,
                0.45654165,  0.62486554],
              [ 0.6143996 ,  0.24072102,  0.4114903 , ...,  1.51608438,
                0.54100887,  0.80509306],
              [ 0.46456858,  0.0884946 ,  0.57334588, ...,  0.41437296,
                0.90743546,  0.78007579]],
      
             [[ 0.63935769,  0.06836551, -0.015311  , ...,  1.15595971,
                1.05760951,  1.2312529 ],
              [ 0.35213352,  0.197653  ,  0.29754935, ...,  0.47394989,
                0.62338563,  0.65766756],
              [ 1.1548429 ,  0.25337811,  0.02290543, ...,  0.4648817 ,
                0.05834947,  1.08793272],
              ...,
              [ 0.34564091,  0.37021532,  0.44659541, ...,  0.42250087,
                0.67991483,  1.07335426],
              [ 0.27292318,  0.6111944 ,  0.6369111 , ...,  0.76217779,
                1.02446786,  0.83080833],
              [ 0.28299893,  0.3752658 ,  0.63134444, ...,  0.64706566,
                0.56957333,  1.0960166 ]]])

  • Indexes: (3)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • brain_hat_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='brain_hat_dim_0'))

  • Attributes: (4)

    created_at :

    2023-08-11T18:53:39.902129

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

  
  
• log_likelihood

  <xarray.Dataset>
  Dimensions:      (chain: 4, draw: 1000, brain_dim_0: 7)
  Coordinates:
    * chain        (chain) int64 0 1 2 3
    * draw         (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
    * brain_dim_0  (brain_dim_0) int64 0 1 2 3 4 5 6
  Data variables:
      brain        (chain, draw, brain_dim_0) float64 -0.7301 -0.5669 ... 1.111
  Attributes:
      created_at:                 2023-08-11T18:53:39.855774
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
    • brain_dim_0: 7
  • Coordinates: (3)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

    • brain_dim_0
      (brain_dim_0)
      int64
      0 1 2 3 4 5 6

      array([0, 1, 2, 3, 4, 5, 6])

  • Data variables: (1)
    • brain
      (chain, draw, brain_dim_0)
      float64
      -0.7301 -0.5669 ... 0.746 1.111

      array([[[-7.30068341e-01, -5.66897907e-01, -8.51724842e-01, ...,
               -6.38261315e-01, -1.01386095e+00, -1.50717005e+00],
              [ 1.20173589e-01,  1.18036313e-01,  1.36024235e-01, ...,
               -5.73828167e+00,  6.65951965e-02,  1.14492434e-01],
              [-7.81080838e-02, -2.83674445e-03, -7.25588796e-02, ...,
               -2.27205375e-02, -5.56370418e-03, -3.13203502e+00],
              ...,
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01],
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01],
              [ 1.31591011e+00, -4.01506396e-01,  1.09042304e+00, ...,
                9.28784878e-01,  1.42296591e+00,  8.93469865e-01]],
      
             [[ 2.16059186e+00,  1.11555375e+00,  1.47677427e+00, ...,
                2.05164561e+00,  2.02605458e+00,  1.72813531e+00],
              [ 1.77388096e+00,  1.13191083e+00,  6.93691124e-01, ...,
                2.09716635e+00,  2.09746634e+00,  1.38138042e+00],
              [ 1.97953314e+00,  1.10081715e+00,  1.86109520e+00, ...,
                1.86423472e+00,  1.52318641e+00,  1.89803239e+00],
      ...
              [-4.56934270e-01,  3.28585167e-01, -3.38645684e-01, ...,
                3.42711356e-01, -8.31827936e-01, -1.12769600e+00],
              [-1.80487408e-01,  1.67077330e-01,  4.31570453e-01, ...,
               -9.19631222e-01,  3.97617432e-01,  2.97425436e-01],
              [ 5.36582065e-01,  3.98456983e-01, -3.36408697e-01, ...,
               -6.49730780e-01,  3.22418695e-01,  2.47998479e-01]],
      
             [[-2.69706428e-01,  4.84176855e-01, -5.05797947e-01, ...,
                3.20945718e-01,  5.65226674e-02,  2.04763636e-01],
              [-1.04473911e+00,  3.60835046e-01, -8.57527069e-01, ...,
               -1.03604572e-03, -2.19569449e-02,  4.85153863e-01],
              [-2.63922705e-01,  2.93179724e-01, -1.55978078e-01, ...,
                3.57093938e-01, -9.68098218e-03,  2.20569887e-01],
              ...,
              [ 9.91736278e-01,  1.20006130e+00,  1.18983165e+00, ...,
                1.19852327e+00,  7.46731041e-01,  1.19333716e+00],
              [ 3.70057543e-01,  3.75356947e-01,  1.25860825e+00, ...,
               -5.65829205e-03,  1.02278603e+00,  1.10344595e+00],
              [ 5.07617798e-01,  1.06876389e+00,  1.11096469e+00, ...,
                4.69727833e-01,  7.46047704e-01,  1.11059478e+00]]])

  • Indexes: (3)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

    • brain_dim_0
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64', name='brain_dim_0'))

  • Attributes: (4)

    created_at :

    2023-08-11T18:53:39.855774

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

  
  
• sample_stats

  <xarray.Dataset>
  Dimensions:          (chain: 4, draw: 1000)
  Coordinates:
    * chain            (chain) int64 0 1 2 3
    * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
  Data variables:
      acceptance_rate  (chain, draw) float64 0.9942 0.9932 1.0 ... 0.7437 0.6009
      step_size        (chain, draw) float64 0.02283 0.02283 ... 0.01823 0.01823
      tree_depth       (chain, draw) int64 6 7 5 4 8 6 5 4 5 ... 5 6 7 7 5 7 8 7 7
      n_steps          (chain, draw) int64 63 159 31 31 255 ... 47 127 255 255 191
      diverging        (chain, draw) bool False False False ... False False False
      energy           (chain, draw) float64 2.459 5.23 0.8842 ... -7.189 -5.73
      lp               (chain, draw) float64 -1.21 0.03107 2.038 ... 10.68 9.605
  Attributes:
      created_at:                 2023-08-11T18:53:39.807300
      arviz_version:              0.15.1
      inference_library:          stan
      inference_library_version:  3.7.0
      num_chains:                 4
      num_samples:                1000
      num_thin:                   1
      num_warmup:                 1000
      save_warmup:                0

  xarray.Dataset

  • Dimensions:
    • chain: 4
    • draw: 1000
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0 1 2 3

      array([0, 1, 2, 3])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 995 996 997 998 999

      array([  0,   1,   2, ..., 997, 998, 999])

  • Data variables: (7)
    • acceptance_rate
      (chain, draw)
      float64
      0.9942 0.9932 1.0 ... 0.7437 0.6009

      array([[9.94233707e-01, 9.93165704e-01, 1.00000000e+00, ...,
              2.58318986e-01, 1.48519049e-04, 6.71099767e-02],
             [7.70774184e-01, 1.80592293e-02, 2.50854737e-01, ...,
              2.98825241e-01, 8.26983265e-01, 4.41928941e-01],
             [9.85851276e-01, 9.91385247e-01, 9.79344898e-01, ...,
              8.60362083e-01, 6.29604725e-01, 6.21876881e-01],
             [9.95387414e-01, 9.99909983e-01, 9.99330539e-01, ...,
              9.87221552e-01, 7.43663516e-01, 6.00850499e-01]])

    • step_size
      (chain, draw)
      float64
      0.02283 0.02283 ... 0.01823 0.01823

      array([[0.02283011, 0.02283011, 0.02283011, ..., 0.02283011, 0.02283011,
              0.02283011],
             [0.00923471, 0.00923471, 0.00923471, ..., 0.00923471, 0.00923471,
              0.00923471],
             [0.02833399, 0.02833399, 0.02833399, ..., 0.02833399, 0.02833399,
              0.02833399],
             [0.01823457, 0.01823457, 0.01823457, ..., 0.01823457, 0.01823457,
              0.01823457]])

    • tree_depth
      (chain, draw)
      int64
      6 7 5 4 8 6 5 4 ... 6 7 7 5 7 8 7 7

      array([[6, 7, 5, ..., 1, 1, 1],
             [3, 6, 6, ..., 4, 7, 4],
             [8, 8, 7, ..., 6, 6, 5],
             [6, 5, 6, ..., 8, 7, 7]])

    • n_steps
      (chain, draw)
      int64
      63 159 31 31 ... 127 255 255 191

      array([[ 63, 159,  31, ...,   3,   2,   3],
             [ 15,  63,  63, ...,  15, 127,  17],
             [255, 511, 223, ...,  63,  63,  63],
             [ 63,  31, 127, ..., 255, 255, 191]])

    • diverging
      (chain, draw)
      bool
      False False False ... False False

      array([[False, False, False, ...,  True,  True,  True],
             [False, False, False, ..., False, False,  True],
             [False, False, False, ..., False, False, False],
             [False, False, False, ..., False, False, False]])

    • energy
      (chain, draw)
      float64
      2.459 5.23 0.8842 ... -7.189 -5.73

      array([[  2.45889561,   5.23014587,   0.8842482 , ...,  -5.24178702,
               -7.52119165,  -8.22620056],
             [-12.63637198, -12.02113756, -11.70029831, ..., -13.51513333,
              -13.30583019,  -3.70330084],
             [  3.81284024,  12.21204895,  12.16631997, ...,   0.12223333,
                1.31505589,  -4.03915439],
             [ -2.14973909,  -2.49191708,  -0.2733382 , ...,  -6.040826  ,
               -7.18920473,  -5.72972827]])

    • lp
      (chain, draw)
      float64
      -1.21 0.03107 2.038 ... 10.68 9.605

      array([[-1.2099401 ,  0.0310734 ,  2.03763653, ..., 10.35927788,
              10.35927788, 10.35927788],
             [17.94392058, 16.07488155, 14.50387307, ..., 16.51494071,
              14.95817912, 13.73149783],
             [-0.84080971, -7.14573667, -4.55199362, ...,  1.82542767,
               5.26002971,  6.31266796],
             [ 5.66941622,  3.1314764 ,  4.76632921, ..., 10.95431518,
              10.68023411,  9.60531483]])

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Int64Index([0, 1, 2, 3], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Int64Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
                  ...
                  990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
                 dtype='int64', name='draw', length=1000))

  • Attributes: (9)

    created_at :

    2023-08-11T18:53:39.807300

    arviz_version :

    0.15.1

    inference_library :

    stan

    inference_library_version :

    3.7.0

    num_chains :

    4

    num_samples :

    1000

    num_thin :

    1

    num_warmup :

    1000

    save_warmup :

    0

  
  

y_true = d.brain_std.values
y_pred = data5.posterior_predictive.stack(sample=("chain", "draw"))["brain_hat"].values.T
az.r2_score(y_true, y_pred)

r2        0.672509
r2_std    0.166309
dtype: float64

aa = az.loo(samples_5, pointwise=True)

/home/rodolpho/Projects/bayesian/BAYES/lib/python3.8/site-packages/arviz/stats/stats.py:803: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

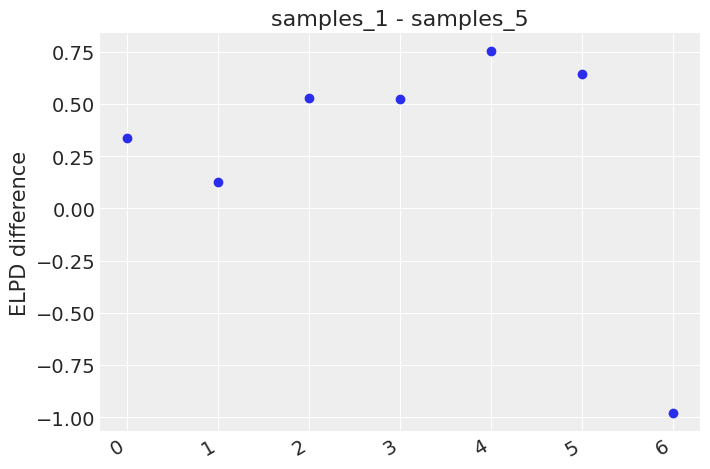
az.plot_elpd({'samples_1':samples_1, 'samples_5': samples_5}, xlabels=True)
plt.show()

/home/rodolpho/Projects/bayesian/BAYES/lib/python3.8/site-packages/arviz/stats/stats.py:803: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(

aaa = data.posterior_predictive.brain_hat[0].values
np.log(np.sum(np.exp(aaa.T), 1)) - np.log(1000)

array([0.50019162, 0.61303674, 0.6133973 , 0.44845226, 0.79786415,
       2.0166922 , 7.29542366])

R Code 7.16

Just using Rethinking Packages - pag 213

R Code 7.17

Just using Rethinking Packages - Pag 213

R Code 7.18

Just using Rethinking Packages - pag 214

---

previous

6 - Os DAGs assombrados & O Terror Causal

next

8 - Os peixes-bois condicionais