3- Modelos Geocêntricos¶
Distribuição Normal¶

fonte: wikipedia
fonte: Distribuição Gausiana
Aula - Statistical Rethinking Winter 2019 Lecture 03
Regressão Linear¶
São simples golems estatísticos.
Modelo de média e variância normalmente (Gaussiano) distribuído.
Média como uma combinação aditiva dos pesos das varáveis que a compõem.
Variância é constante.
Gerando um processo de flutuação normal¶
Através da flutuação normal (sobe 1 ou desce 1) iremos construir um processo que tenha como resultante natural o surgimento de um comportamento cuja distribuição podemos descrever como a normal.
# Necessário para desbloquear o asyncio no Jupyter
# Fonte: https://pystan.readthedocs.io/en/latest/faq.html
# Fonte: https://github.com/microsoft/playwright-python/issues/178
# Docs Pystan: https://pystan.readthedocs.io/en/latest/index.html
# -------------
# Instalar nest_asyncio: pip install nest_asyncio - Estára no requirements.txt
# Versões
# python==3.8.0
# numpy==1.21.1
# pystan==3.2.0
# nest_asyncio==1.5.1
# -------------
# Rodar esse comando antes de import a stan (pystan versão 3.x)
import nest_asyncio
nest_asyncio.apply()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# Add fonts to matplotlib to run xkcd
from matplotlib import font_manager
font_dirs = ["fonts/"] # The path to the custom font file.
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)
for font_file in font_files:
font_manager.fontManager.addfont(font_file)
# plt.xkcd()
# Construindo um passeio conforme a distribuição Bernoulli(0.5) em +1 ou -1
n_linhas = 500 # Quantas linhas iremos simular?
n_passos = 30 # Quantidade de passos que iremos simular?
corte_1 = 3 # Indica o primeiro corte no passeio
corte_2 = 14 # Indica o segundo corte no passeio
corte_3 = 26 # Indica o terceiro corte no passeio
aleatorizar_grafico = True # True para ver a simulação um pouco mais aleatorizada visualmente. False para ver sem efeito.
passeios = [] # Armazenar todos os passeios gerados num array
# Parâmetros da simulação
plt.figure(figsize=(17, 9))
plt.rcParams['axes.facecolor'] = 'lightgray' # Alterando a cor de fundo, para ficar mais elegante.
for linha in range(n_linhas): # Quantas linhas iremos plotar
passeio = [0] # Inicializando todos os pontos com o valor 0 (conforme dito acima!)
novo_ponto = 0 # variável de controle
for passo in range(n_passos): # Quantos passos iremos simular?
if aleatorizar_grafico:
# +1 (subida) ou -1 (descida) - Com efeito de aleatorizacão (apenas para melhorar a visualização).
novo_ponto = novo_ponto + np.random.uniform(1, -1)
else:
# +1 (subida) ou -1 (descida) - Sem efeito de aleatorizacão - "Pixelizado"
novo_ponto = novo_ponto + np.random.choice([1, -1])
passeio.append(novo_ponto)
passeios.append(passeio) # Armazendo todas as linhas geradas
plt.plot(passeios[linha], color='darkblue', alpha=0.5, linewidth=0.1) # Plotando a linha gerada
# Retas horizontais dos cortes
plt.vlines(corte_1, -15, 15, color='darkred', ls='--', linewidth=3)
plt.vlines(corte_2, -15, 15, color='orange', ls='--', linewidth=3)
plt.vlines(corte_3, -15, 15, color='darkgreen', ls='--', linewidth=3)
# Configurando infos do gráfico
plt.title("Passeio Aleatório {+1, -1} com p(0.5)")
plt.xlabel('Número de passos')
plt.ylabel('Valor')
plt.grid(axis='y', ls='--', color='white')
plt.show()
passeios = np.array(passeios).T # Transpondo os vetores de passeios para ajuste na plotagem.
# ------------
# Gerando os histogramas de todas as linhas para alguns passos específicos ao longo do passeio.
fig, [ax1, ax2, ax3] = plt.subplots(1, 3, figsize=(17, 6))
ax1.hist(passeios[corte_1], color='darkred', rwidth=0.8, density=True)
ax1.grid(axis='y', ls='--', color='white')
ax1.set_title("Histograma \n Normalmente distribuído \n passo " + str(corte_1))
ax1.set_xlabel('Valor')
ax1.set_xlim(-20, 20)
ax1.set_ylim(0, 0.25)
ax2.hist(passeios[corte_2], color='darkorange', rwidth=0.8, density=True)
ax2.grid(axis='y', ls='--', color='white')
ax2.set_title("Histograma \n Normalmente distribuído \n passo " + str(corte_2))
ax2.set_xlabel('Valor')
ax2.set_xlim(-20, 20)
ax2.set_ylim(0, 0.25)
ax3.hist(passeios[corte_3], color='darkgreen', rwidth=0.8, density=True)
ax3.grid(axis='y', ls='--', color='white')
ax3.set_title("Histograma \n Normalmente distribuído \n passo " + str(corte_3))
ax3.set_xlabel('Valor')
ax3.set_xlim(-20, 20)
ax3.set_ylim(0, 0.25)
plt.show()
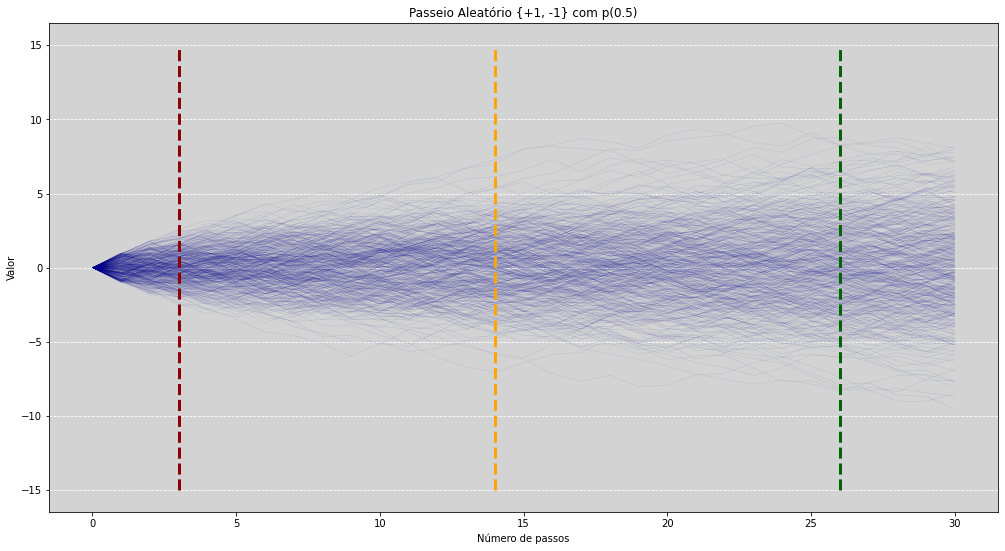
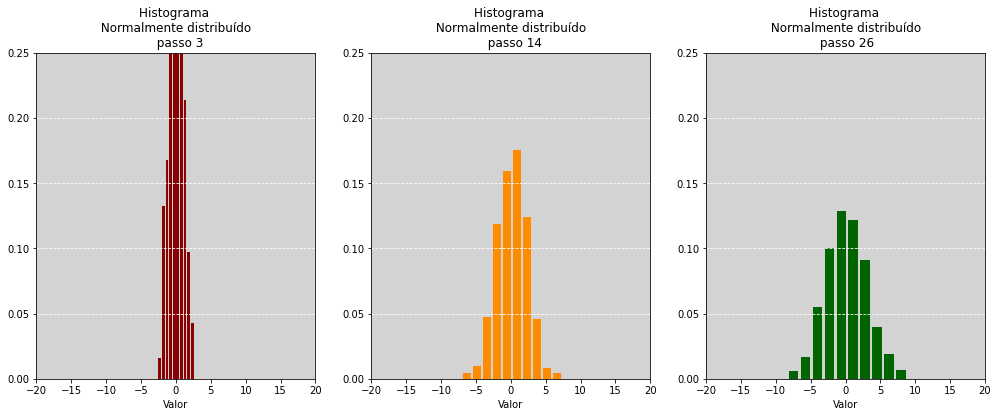
Todas as flutuações geradas se equilibriam entre si, gerando assim uma curva simétrica. Porém cada uma delas individualmente, e não necessariamente, se equilibram entre si. Isso é a \(Normal\)!
Porque a Normal?¶
O interessante, e frustrante ao mesmo tempo, é que mesmos nós sabendo como cada uma das curvas são geradas, não temos acesso a como cada uma delas individualmente faz o seu percurso, pois temos muito pouca informação sobre como é o processo gerador dessas curvas.
Assim, quando vimos um comportamento de um evento que é normalmente distribuído, por exemplo, não sabemos o que tem la dentro! Não temos um acesso intuitivo da informação contida no comportamento individual de cada passeio.
Mas sabendo que o processo como um todo tem o comportamento, aproximadamente, normalmente distribuído, podemos usar essa informação para falsificar ou não hipóteses de um estudo particular.
E isso é muito legal, pois podemos descrever o processo como um todo, com apenas por dois números, pois toda a informação do funcionamento da maquinaria subjacente do processo foi eliminada. E tudo que foi preservado foi a média (\(\mu\)) e o desvio padrão (\(\sigma\)), por isso que precisamos apenas desses dois números para descrever uma distribuição normal.
Note
Essa é toda a informação que conseguimos extrair da maquinaria subjacente, a Natureza!
O mais terrível é que não podemos saber o funcionamento do processo a partir de um simples histograma! Temos que realmente fazer ciência para isso, temos de cavar mais fundo, medir coisas mais difíceis para só assim descobrir mais algumas coisas nas profundezas do mecanismo de geração do processo.
Isso é verdade não apenas para a \(Normal\), mas para muitas outras distribuições! Todas as distribuições de máxima entropia tem essa mesma propriedade, que muitos processos diferentes possuem a mesma distribuição de frequências.
Perspectiva Ontológica¶
Ontologia é o ramo da filosofia que estuda a natureza do ser, da existência e da própria realidade. Vamos observar a distribuição \(Normal\) sobre uma perspectiva ontológia:
Processo que adiciona flutuações amortecidas como resultado.
As flutuações amortecidas se aproximam de uma gaussiana.
Mas nenhuma informação sobrou do processo gerador, apenas a média e a variância.
Não podemos inferir o processo a partir dessa distribuição.
Se quisermos construir um modelo visando responder de modo mais conservador possível, no qual tudo que estiver disposto a dizer sobre algum conjunto de medidas, como medida de alturas, é que eles têm variância finita e podemos usar a distribuição gaussiana.
Mesmo se eles forem distorcidos ou alguma outras coisas, a distribuição gaussiana cobrirá uma faixa mais ampla de valores do que qualquer outra com a mesma média e a mesma variância!
Essa é a distribuição mais é conservadora que podemos assumir. Qualquer outra distribuição será mais restrita por isso terá mais informação incorporada, por isso a opção mais conservadora que podemos propor é a gaussiana, no qual tudo que precisamos para ela é a média a variância. (Isso será demostrado mais para frente no curso.)
Perspectiva Epistemologica¶
Epistemologia, também conhecida como a Teoria do Conhecimento, é o ramo da filosofia que estuda como o ser humano ou a própria ciência adquire e justifica seus conhecimentos. Vamos observar a \(Normal\) sobre essa perspectiva:
Conhecemos apenas a média e a variância.
A menos surpreendente e mais conservadora (máxima entropia) distribuição gaussiana.
É a distribuição natural da máxima entropia.
Modelos Lineares¶
“Modelo lineares generalizados”: teste t, regressão simples, regressão multipla, ANOVA, ANCOVA, MANOVA, MANCOVA, etc, etc, etc. Todos esses modelos são a mesma coisa, são todos modelos os lineares.
A seguir, iremos construir modelos lineares manualmente e do zero para entendermos como é o processo de pensamento de construção de hipóteses e, também, iremos construir um gráfico no qual iremos visualizar a nossa incerteza do sistema.
Warning
Iremos aprender estratégias e não procedimentos!
Acordando a linguagem que iremos trabalhar¶
Relembrando o primeiro modelo que nós fizemos anteriormente, o lançamento do globo, nós tinhamos:
\(w\): Resultado
\(\sim\): “É distribuído como…”
\(Binomial( N, p)\): É a função de distribuição de probabilidade dos dados (verossimilhança, ou likelihood no inglês)
\(p\): É o parâmetro que iremos estimar
\(Uniform(0, 1)\): Nossa distribuição à priori
No exemplo do lançamento do globo, o que estávamos interessados em saber era a proporção de água na superfície (\(p\)) da Terra. O processo que usamos para coletar os dados, a amostragem, automaticamente nos propõem, de modo quase impositivo, a utilização da estrutura Binomial.
A estrutura que distribui os dados binominalmente, nada mais é do que a contagem do número de vezes que é possível acontecer tal fato, dado que a proporção \(p\) é fixa para todas às vezes \(N\) que iremos retirar uma amostra.
Essa é a linguagem que iremos usar nesse curso. A notação matemática padrão, na qual consiste em uma maneira de comunicar a todos os nossos colegas de trabalho o que foi pensado, quais foram as suposições, quais foram as hipóteses (isto é, as sugestões) e, também, qual a estrutura foi proposta para um possível caminho para se entender o problema.
Note
A linguagem matemática será a forma de comunicar ao mundo sua forma de pensar!
Linguagem da modelagem¶
Do mesmo modo que escrevemos o modelo acima iremos escrever todos os outros modelos, inclusive, a programação usando a linguagem probabilística Stan, o qual tem a sua sintaxe próxima a esse formato.
Para qualquer modelo que iremos elaborar, seja uma regressão linear simples ou modelos mais elaborados, temos que criar uma lista com todas as variáveis que irão participar desse modelo. Algumas coisas que iremos observar nos dados, como a contagem do número de vezes que o globo foi lançado. E também haverá outras coisas que não vamos poder observar, como a inclinação de uma reta de uma modelo linear simples, ou proporção de água no globo, pois elas não são entidades observáveis.
Por isso temos que listar todas as variáveis e então defini-las.
Listando as variáveis:
Um modelo de regressão, assim como qualquer outro modelo, será escrito da mesma forma que vimos anteriormente, porém esse modelo terá muito mais símbolos pois temos muito mais variáveis participando da explicação, mas é a mesma coisa, apenas precisamos definir a cada um desses símbolos.
O motor dos modelos de regressão linear é a segunda linha da definição abaixo (a seguir iremos construir esse modelo desde o início):
Essa segunda linha, \( \mu_i = \beta x_i \), geralmente a parte que é mais confusa para se entender (iremos ver um exemplo a seguir), mas ela significa que média da distribuição normal de cima (média do \(y_i\)) é geralmente definida por uma equação, o que define em termos de alguma outra variável que observamos, \(x_i\).
O \(x_i\) é uma variável que ajuda a explicar o comportamento do \(y_i\), ou seja, \(x_i\) é uma variável explicativa.
Mas repare que \(x_i\) também tem uma distribuição, nós normalmente não nos preocupamos em definir uma distribuição para as variáveis explicativas, pois não iremos prevê-las, porém existe uma grande vantagem em fazer essas suposições de distribuição, pois podemos fazer coisas muito legais com esse fato, iremos ver essas coisas mais à frente, tais como medidas de erros e também dados faltantes.
Assim, como todas as variáveis têm sua própria definição de distribuição, se você não sabe algo sobre algumas delas podemos colocar dentro do modelo e assim iremos ganhar automaticamente um poder inferencial do que estávamos perdendo antes.
Construíndo um Modelo Linear¶
Com o conjunto de dados amostrados de uma população, extraída do livro da Nancy Howel, Life history of the DOBE !KUNG, um novo clássico de demografia evolucionária, disponível no pacote R rethinking e suas versões variantes. (Nesse material temos uma cópia do link Rethinking - R-library - GitHub.

Estudo Descritivo da Base de Dados¶
df = pd.read_csv('data/Howell1.csv', sep=';') # Banco de dados do pacote Rethinking - Disponível no Github
# Just adults
df = df[df.age >= 18 ]
# =======================================
# Página 86
# Overthinking: Sample size and the normality of sigma's posterior
# Note que, no gráfico posteriori da conjunta, o sigma não é normal.
overthinking_test = False
qtd_sampled = 5
# Amostragem dos dados
if overthinking_test:
sample_df = np.random.uniform(0, len(df), qtd_sampled)
df = df.iloc[sample_df, :]
# =======================================
print(df.describe()) # Resumo do banco de dados
height weight age male
count 352.000000 352.000000 352.000000 352.000000
mean 154.597093 44.990486 41.138494 0.468750
std 7.742332 6.456708 15.967855 0.499733
min 136.525000 31.071052 18.000000 0.000000
25% 148.590000 40.256290 28.000000 0.000000
50% 154.305000 44.792210 39.000000 0.000000
75% 160.655000 49.292693 51.000000 1.000000
max 179.070000 62.992589 88.000000 1.000000
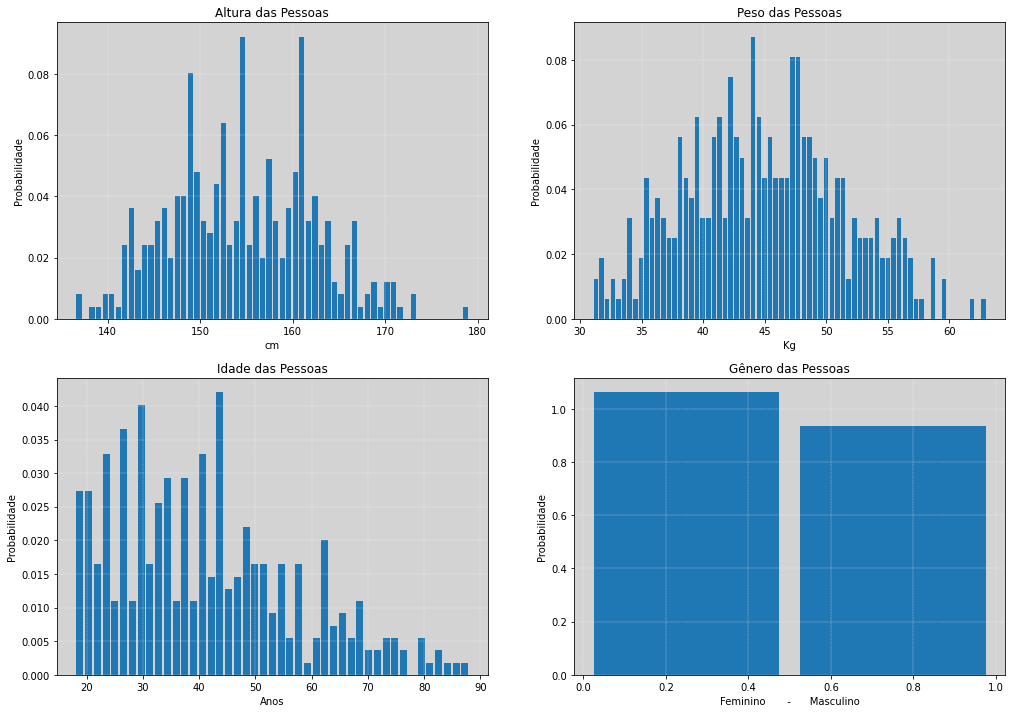
Nosso conjunto de dados contém um total de \(544\) indivíduos, abaixo temos um histograma descritivo das quatro variáveis da base:
Altura (height)
Peso (weight)
Idade (Age)
Gênero (male) - Definido \(1\) para homens e \(0\) para mulheres
# Plotando os histogramas
plt.rcParams['axes.facecolor'] = 'lightgray'
fig, [[ax1, ax2], [ax3, ax4]] = plt.subplots(2,2, figsize=(17, 12))
# Histograma de todos os dados da altura (height)
ax1.hist(df.height, bins=60, density=True, rwidth=0.8)
ax1.set_title('Altura das Pessoas')
ax1.set_xlabel('cm')
ax1.set_ylabel('Probabilidade')
ax1.grid(color='white', linewidth='0.3', ls='--')
# Histograma de todos os dados do peso (weight)
ax2.hist(df.weight, bins=70, density=True, rwidth=0.8)
ax2.set_title('Peso das Pessoas')
ax2.set_xlabel('Kg')
ax2.set_ylabel('Probabilidade')
ax2.grid(color='white', linewidth='0.3', ls='--')
# Histograma de todos os dados da idade (age)
ax3.hist(df.age, bins=45, density=True, rwidth=0.8)
ax3.set_title('Idade das Pessoas')
ax3.set_xlabel('Anos')
ax3.set_ylabel('Probabilidade')
ax3.grid(color='white', linewidth='0.3', ls='--')
# Histograma de todos os dados da gênero (male)
ax4.hist(df.male, bins=2, density=True,rwidth=0.9)
ax4.set_title('Gênero das Pessoas')
ax4.set_xlabel('Feminino - Masculino')
ax4.set_ylabel('Probabilidade')
ax4.grid(color='white', linewidth='0.3', ls='--')
plt.show()
Modelos Gaussianos¶
Vamos propor um primeiro modelo, abaixo temos a um modelo \(Normal\):
A altura \(h\) do indivíduo \(i\) será distribuído normalmente, com uma média \(\mu\) e o desvio padrão \(\sigma\).
Estamos usando as letras gregas \(\mu\) e \(\sigma\), por convenção de linguagem, mas nada nos impede de usarmos quaisquer outros símbolos. Não haverá nenhum problema, apenas iremos irritar alguns estatísticos, mas isso será mais um bônus!
Aqui é necessário que você saiba ler e entender o que isso significa, só assim você aprenderá o que está acontecendo. Lembre-se isso é apenas uma linguagem, isso não é um código. É apenas uma forma de comunicação, ou seja, é uma comunicação científica.
Aqui temos duas variáveis para estimar, \(\mu\) e \(\sigma\), e teremos que inferir a partir de \(h\), das coisas que medimos, mas \(\mu\) e \(\sigma\) precisam de definições por que esse é um modelo bayesiano.
Adicionando prioris¶
Agora vamos definir uma priori para os parâmetros da \(Normal\), o \(\mu\) e o \(\sigma\):
# Plotando a distribuição à priori do mu e do sigma
plt.rcParams['axes.facecolor'] = 'lightgray'
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(15, 8))
x_mu = np.arange(90, 270, 1)
x_sigma = np.arange(-10, 60)
# Priori do mu
ax1.plot(x_mu, stats.norm(178, 20).pdf(x_mu))
ax1.set_title('Priori de $\mu$ \n Normal(178, 20)')
ax1.grid(color='white', linewidth='0.3', ls='--')
#Priori do Sigma
ax2.plot(x_sigma, stats.uniform(0, 50).pdf(x_sigma))
ax2.set_title('Priori de $\sigma$ \n Uniforme(0, 50)')
ax2.grid(color='white', linewidth='0.3', ls='--')
plt.show()
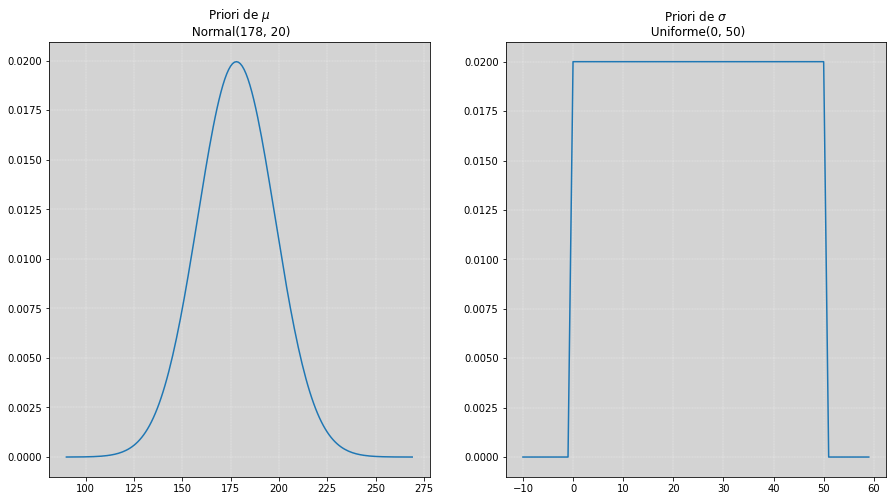
Qual é a implicação de usar essas distribuições para \(\mu\) e \(\sigma\)?
O valor \(178\) foi escolhido para ser a média da distribuição normal (à priori), esse valor foi escolhido por acharmos que poderia ser a altura média da população, e com isso adicionamos uma generosa incerteza (incerteza da média) de \(20\) (gráfico da esquerda).
Para o \(\sigma\) colocamos qualquer valor entre \(0\) até \(50\) (gráfico da direita), esses valores têm igual probabilidade de ocorrer, esse é um range bastante razoável já que \(50\) é um valor bem mais alto do que podemos esperar para o desvio padrão, pois não temos uma nenhuma informação mais razoável para colocar como priori (no mundo real certamente saberíamos um pouco mais).
Simulação a partir da priori¶
O que essas prioris estão implicando sobre a estimativa da altura, antes de vermos os dados (\(h\))?
Para saber, vamos Simular! Distribuição à Priori Preditiva.
Simular os dados apenas das prioris nos permitirá entender se, do modo como estamos ensinando o modelo, seu resultado está sendo satisfatório.
Vamos simular!
# ========================================================================
# Construindo o processo de amostragem da distribuição à priori preditiva.
# *** Priori versão com dados absurdos ***
# ========================================================================
# Amostragem
amostra_mu = stats.norm(178, 20).rvs(10000) # Amostra da Normal(178, 20) estimativa para mu.
amostra_sigma = stats.uniform(0, 100).rvs(10000) # Amostra da Uniforme(0, 50) estimativa para sigma.
amostra_h_priori = stats.norm(amostra_mu, amostra_sigma).rvs() # Amostrando da Normal(mu, sigma)
# Plot
plt.rcParams['axes.facecolor'] = 'lightgray'
plt.figure(figsize=(17, 7))
plt.hist(amostra_h_priori, density=True, bins=170, rwidth=0.8)
plt.title('Distribuição Preditiva da Priori com Valores Absurdos \n Altura \n $Normal(178, 100)$')
plt.xlabel('(cm)')
plt.ylabel('Probabilidade')
plt.vlines(0, 0, 0.008, color='red', ls='--', linewidth=2) # 0 cm de altura, ovo fertilizado.
plt.vlines(272, 0, 0.008, color='red', ls='--', linewidth=2) # 272 cm de altura, pessoa mais alta da história.
plt.grid(color='white', linewidth='0.3', ls='--')
plt.show()
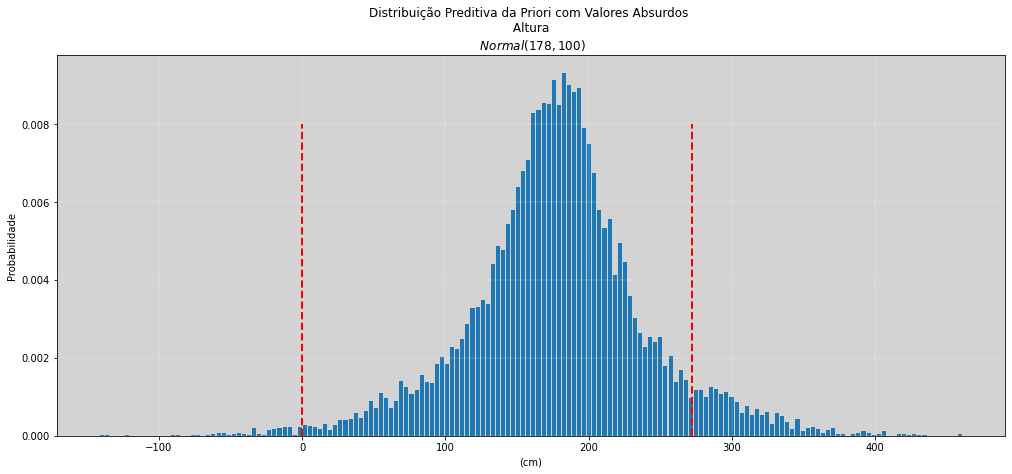
Plotar o gráfico da Distribuição Preditiva da Priori nos permite observar que a probabilidade, por exemplo, de alguém ter a altura próxima de \(0 cm\) é praticamente igual a zero, \(P\{altura = 0\}\), e ,também, a probabilidade de uma pessoa ser maior do que \(272 cm\), \(P\{altura >= 272\}\), que é a altura da pessoa mais alta no mundo já registrada, é bem baixa.
Imagine agora que colocaremos como à priori valores muito absurdos para o \(\sigma\), vamos ver o que acontece:
# ========================================================================
# Construindo o processo de amostragem da distribuição à priori preditiva.
# ========================================================================
# Amostragem
amostra_mu = stats.norm(178, 20).rvs(10000) # Amostra da Normal(178, 20) estimativa para mu.
amostra_sigma = stats.uniform(0, 50).rvs(10000) # Amostra da Uniforme(0, 50) estimativa para sigma.
amostra_h_priori = stats.norm(amostra_mu, amostra_sigma).rvs() # Amostrando da Normal(mu, sigma)
# Plot
plt.rcParams['axes.facecolor'] = 'lightgray'
plt.figure(figsize=(17, 7))
plt.hist(amostra_h_priori, bins=171, rwidth=0.8, density=True)
plt.title('Distribuição Preditiva da Priori \n Altura')
plt.xlabel('(cm)')
plt.ylabel('Probabilidade')
plt.vlines(0, 0, 0.008, color='red', ls='--', linewidth=2) # 0 cm de altura, ovo fertilizado.
plt.vlines(272, 0, 0.008, color='red', ls='--', linewidth=2) # 272 cm de altura, pessoa mais alta da história.
plt.grid(color='white', linewidth='0.1', ls='--')
plt.show()
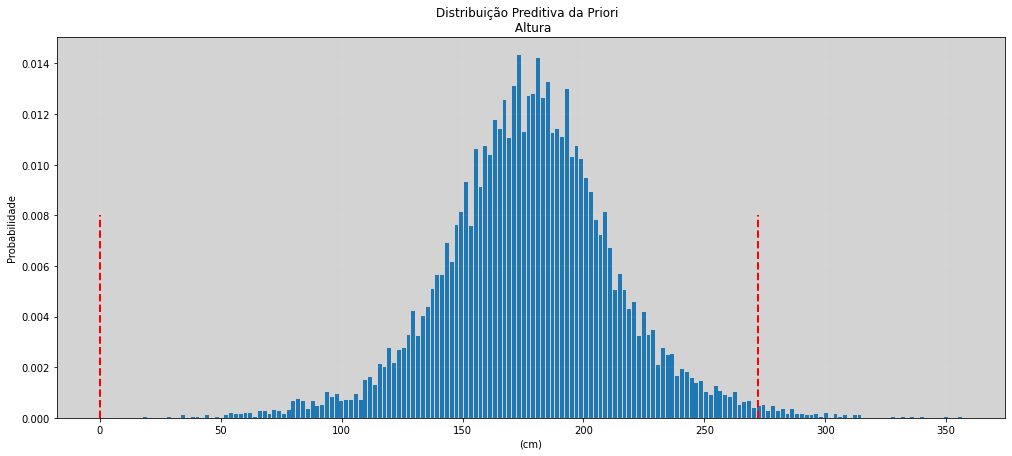
Os valores de probabilidade que estão sendo atribuídos pela distribuição à priori e que estão para fora dos limites mais conservadores possíveis, não deveriam ter uma importância tão grande, ou seja, sua probabilidade deveria se aproximar de zero!
Esse é um exemplo de escolha ruim para uma priori, colocando apenas um valor enorme para \(\sigma\) mas sem ter uma ligação mais íntima com a natureza do problema.
Nesse caso, o caso univariado, as distorções que podem ser geradas por usarmos uma priori dessa forma é praticamente nula, o modelo provavelmente ajustará bem. Já para modelos mais complexos, como modelos mistos ou modelos hierárquicos com muitos parâmetros, a utilização de prioris sem muito sentido pode causar sérias distorções nos resultados.
Por isso, sempre simule a priori para observar se o comportamento do modelo condiz com a realidade.
Note
Priori: é essa a nossa crença antes do modelo ver o dados!
Calculando a Posteriori Conjunta¶
Nosso objetivo é estimar a distribuição conjunta dos parâmetros \(\mu\) e \(\sigma\), para isto, iremos calcular a estimativa pelo método do grid de aproximação.
# Para visualização das multiplicações vamos deixar o 𝜎 fixo, em 20, por exemplo,
# e iremos variar o 𝜇 entre 100 e 300, para os três valores distintos de alturas (147, 155, 180).
curva_1 = 0 # Resetando a variável curva_1
curva_2 = 0 # Resetando a variável curva_2
curva_3 = 0 # Resetando a variável curva_3
posteriori = np.array([])
for mu in np.arange(100, 300, 1):
curva_1 = np.append(curva_1, stats.norm(mu, 20).pdf(147)) # Para todos os 𝜇, calcular a probabilidade de ocorrer 147 com sigma fixo.
curva_2 = np.append(curva_2, stats.norm(mu, 20).pdf(155)) # Para todos os 𝜇, calcular a probabilidade de ocorrer 155 com sigma fixo.
curva_3 = np.append(curva_3, stats.norm(mu, 20).pdf(180)) # Para todos os 𝜇, calcular a probabilidade de ocorrer 180 com sigma fixo.
# Plot
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 7))
ax1.plot(np.arange(100, 301), curva_1, color='darkgreen')
ax1.plot(np.arange(100, 301), curva_2, color='darkorange')
ax1.plot(np.arange(100, 301), curva_3, color='red')
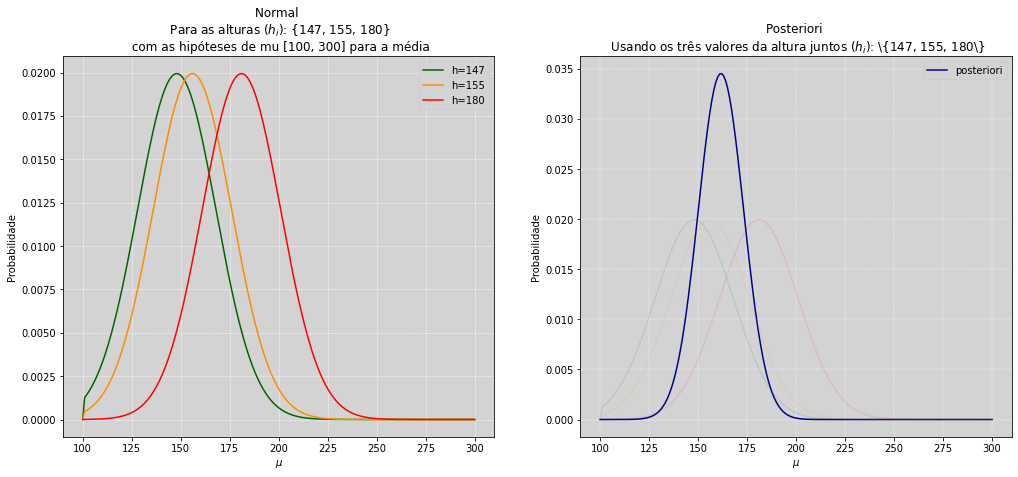
ax1.set_title('Normal \n Para as alturas ($h_i$): {147, 155, 180} \n com as hipóteses de mu [100, 300] para a média')
ax1.set_xlabel('$\mu$')
ax1.set_ylabel('Probabilidade')
ax1.grid(color='white', linewidth='0.5', ls='--')
ax1.legend(['h=147', 'h=155', 'h=180'])
# Abaixo iremos fazer a soma dos logs, ao invés de multiplicar. Isso será feito na próxima célula.
# posteriori_nao_normalizada = np.log(curva_1) + np.log(curva_2) + np.log(curva_3) #
posteriori_nao_normalizada = curva_1 * curva_2 * curva_3 # Essa multiplicação será feita ponto a ponto.
posteriori = posteriori_nao_normalizada / np.sum(posteriori_nao_normalizada) # Normalizando a posteriori
ax2.plot(np.arange(100, 301), posteriori, color='darkblue') # Essa multiplicação será feita ponto a ponto.
ax2.plot(np.arange(100, 301), curva_1, color='darkgreen', alpha=0.1)
ax2.plot(np.arange(100, 301), curva_2, color='darkorange', alpha=0.1)
ax2.plot(np.arange(100, 301), curva_3, color='red', alpha=0.1)
ax2.set_title('Posteriori \n Usando os três valores da altura juntos ($h_i$): \{147, 155, 180\}')
ax2.set_xlabel('$\mu$')
ax2.set_ylabel('Probabilidade')
ax2.grid(color='white', linewidth='0.4', ls='--')
ax2.legend(['posteriori'])
plt.show()
# ================================
# Calculando a posteriori
# ================================
# Filter only adults (>= 18 years old)
df2 = df[df.age >= 18]
grid = 100 # Determina a precisão, para valores maiores demanda maior custo computacional!
if overthinking_test: # Pag. 86 SR2
grid_width = (142, 162)
grid_height = (2, 20)
else:
grid_width = (153, 156)
grid_height = (7, 8.5)
mu_ls = np.linspace(grid_width[0], grid_width[1], grid) # Espaço do 𝜇 - Esses valores foram escolhidos para uma melhor visualização.
sigma_ls = np.linspace(grid_height[0], grid_height[1], grid) # Espaço do 𝜎 - Esses valores foram escolhidos para uma melhor visualização.
mu, sigma = np.meshgrid(mu_ls, sigma_ls) # Construindo um plano do 𝜇 vs 𝜎.
mu = mu.flatten()
sigma = sigma.flatten()
verossimilhanca = np.array([])
for i in range(grid**2):
verossimilhanca_parcial = stats.norm(mu[i], sigma[i]).pdf(df2.height) # Calcular a verossimilhança para cada (𝜇, 𝜎), usando todas as alturas da amostra.
verossimilhanca_parcial_log = np.log(verossimilhanca_parcial.flatten()) # Calculando o log da verossimilhança
verossimilhanca = np.append(verossimilhanca, np.sum(verossimilhanca_parcial_log))
# Adicionando a priori
# P{ altura | 𝜇, 𝜎} * P{𝜇} * P{𝜎} == exp[ log(P{ altura | 𝜇, 𝜎}) + log(P{𝜇}) + log(P{𝜎}) ]
posteriori_nao_normalizada = verossimilhanca + \
np.log(stats.norm(178, 20).pdf(mu)) + \
np.log(stats.uniform(0, 50).pdf(sigma)) # Priori de sigma
# Explicação na página 561, endnotes número 73! Mais detalhes no gráfico abaixo.
posteriori = np.exp(posteriori_nao_normalizada - max(posteriori_nao_normalizada))
posteriori = posteriori / posteriori.sum()
plt.figure(figsize=(19, 10))
mu_mesh, sigma_mesh = np.meshgrid(mu_ls, sigma_ls, sparse=True)
plt.contourf(mu_mesh.flatten(), sigma_mesh.flatten(), posteriori.reshape((grid, grid)))
plt.xlabel('$\mu$')
plt.ylabel('$\sigma$')
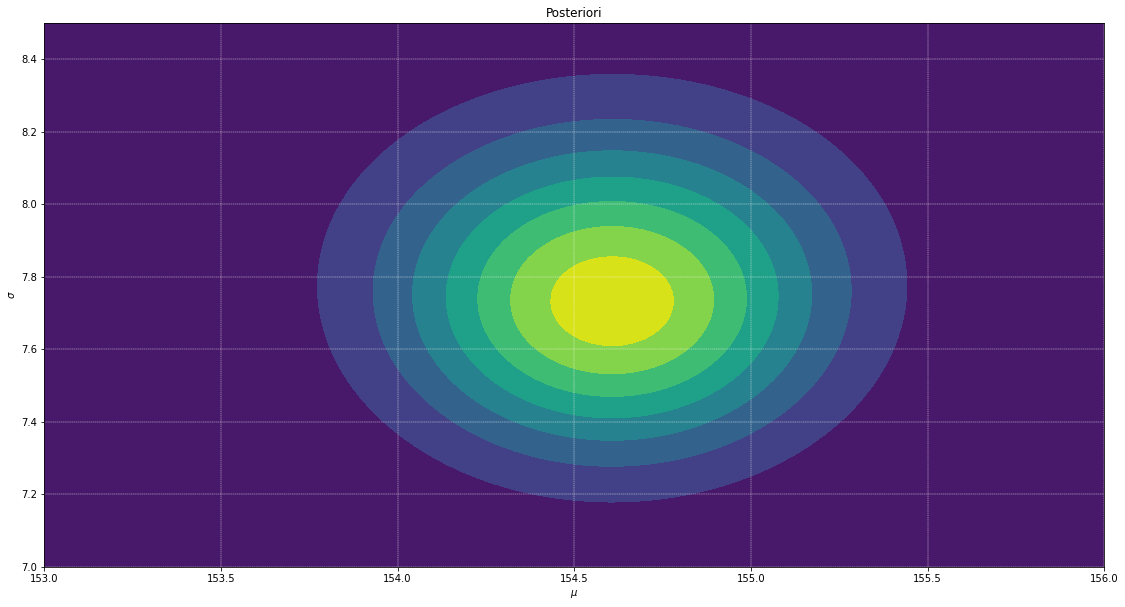
plt.title('Posteriori')
plt.xlim(grid_width[0], grid_width[1])
plt.ylim(grid_height[0], grid_height[1])
plt.grid(ls='--', color='white', linewidth=0.4)
plt.show()
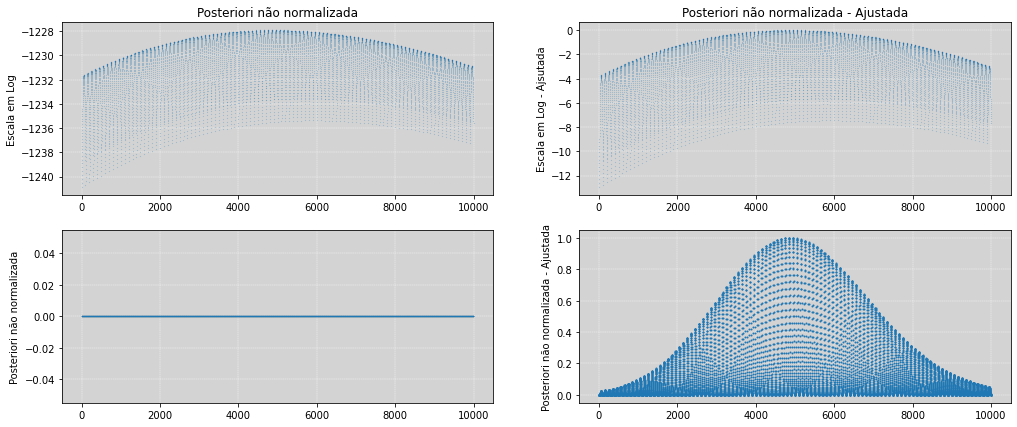
# Explicação gráfica - Não faz parte do material original do curso.
# Porque usar (posteriori_nao_normalizada - np.max(posteriori_nao_normalizada))
# Como exp(-x) -> 0 quando x é muito negativo. Sem normalização, todos os valores serão zero.
# Lembrando que exp(0) = 1, por isso usar o max padroniza os valores.
# Ao gerar a posteriori, a escala dos valores se mantem.
fig, [[ax1, ax2], [ax3, ax4]] = plt.subplots(2, 2, figsize=(17, 7))
# Gráfico 1 e 3
ax1.plot(posteriori_nao_normalizada, 'o', ms=0.1)
ax1.set_title('Posteriori não normalizada')
ax1.set_ylabel('Escala em Log')
ax1.grid(color='white', linewidth=0.4, ls='--')
ax3.plot(np.exp(posteriori_nao_normalizada), 'o', ms=0.1)
ax3.set_ylabel('Posteriori não normalizada')
ax3.grid(color='white', linewidth=0.4, ls='--')
# Gráfico 2 e 4
post_ajustada = (posteriori_nao_normalizada - np.max(posteriori_nao_normalizada))
ax2.plot(post_ajustada, 'o', ms=0.1)
ax2.set_title('Posteriori não normalizada - Ajustada')
ax2.set_ylabel('Escala em Log - Ajsutada')
ax2.grid(color='white', linewidth=0.4, ls='--')
ax4.plot(np.exp(post_ajustada), 'o', ms=1)
ax4.set_ylabel('Posteriori não normalizada - Ajustada')
ax4.grid(color='white', linewidth=0.4, ls='--')
plt.show()
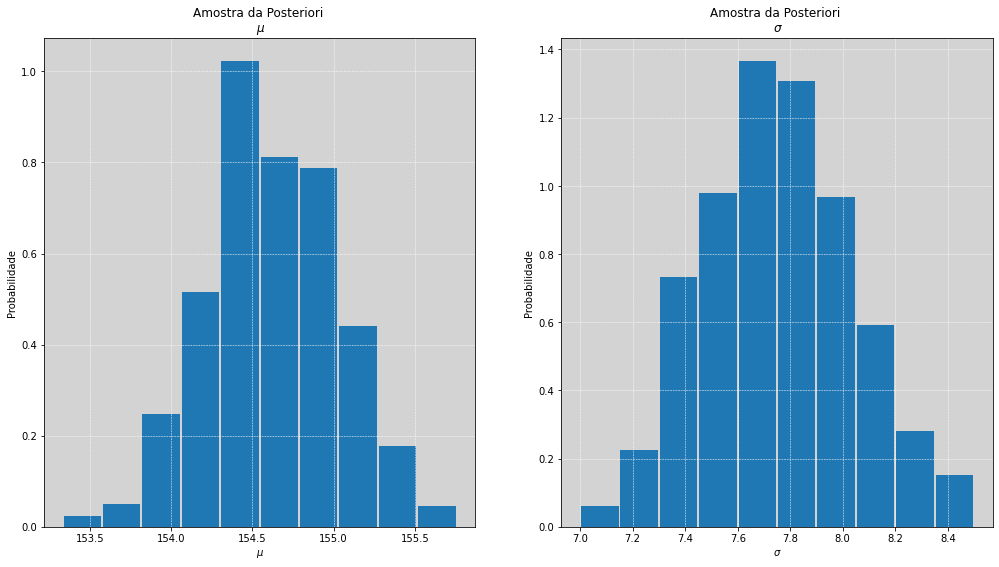
# =================================================================
# Amostrando 𝜇 e o 𝜎 a partir da distribuição à posteriori.
# =================================================================
# Escolhendo pontos 1000 pontos aleatórios dentro do grid com a probabilidade à posteriori
amostras_posteriori_index = np.random.choice(np.arange(grid*grid), size=1000, replace=True, p=posteriori)
mu_amostrado = mu[amostras_posteriori_index]
sigma_amostrado = sigma[amostras_posteriori_index]
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 9))
ax1.hist(mu_amostrado, rwidth=0.95, density=True)
ax1.set_title('Amostra da Posteriori \n $\mu$')
ax1.set_xlabel('$\mu$')
ax1.set_ylabel('Probabilidade')
ax1.grid(color='white', ls='--', linewidth=0.5)
ax2.hist(sigma_amostrado, rwidth=0.95, density=True)
ax2.set_title('Amostra da Posteriori \n $\sigma$')
ax2.set_xlabel('$\sigma$')
ax2.set_ylabel('Probabilidade')
ax2.grid(color='white', ls='--', linewidth=0.5)
plt.show()
Aproximação Quadrática¶
A partir de agora até a metade do curso iremos usar a aproximação quadrática. Se você fez os cálculos da posteriori para a altura, oque é sugerido fortemente, percebemos que a complexidade e o custo computacional envolvido para estimar às duas variáveis (\(\mu\) e \(\sigma\)) são bastante significativos.
Para modelos que necessitem estimar mais parâmetros, \(10\) parâmetros por exemplo, o custo computacional e a estrutura necessária para calcular essa estimativa com o método do grid de aproximação se torna inviável. Por isso temos que pensar em uma nova estrutura na qual podemos, Laplace, \(1749-1827\), propor o uso da aproximação quadrática. Com essa estrutura mais exótica, nós poderemos calcular estimativas da posteriori em dimensões muito elevadas.
Aproximação da posteriori como uma Gaussiana
Podemos construir essa estimativa encontrando o valor das duas seguintes coisas:
Pelo “pico” da posteriori, maximum a posteriori (MAP)
Desvio Padrão e a correlação entre os parâmetros.
As estimativas são bem parecidas com o que já fizemos, exceto que não temos prioris.
A primeira coisa que temos que olhar é para a posteriori (nos histogramas acima) de \(\mu\) e \(\sigma\) e subir a colina até encontrar o pico da distribuição. O computador pode começar a busca por qualquer local sem saber onde está o pico, mas ele sabe subir a colina e então pode simplesmente subir usando o apenas o gradientes descendentes (ou melhor, usando o gradiente ascendente, pois iremos escalar a subida até o pico). Existem muitos algoritmos eficientes para fazer isso, e podemos dar a ele um espaço multidimensional muito alto (bem maior que 2, como no exemplo anterior) e iremos alcançar o pico.
Quando alçarmos o pico, só precisamos medir a curvatura no pico para saber a largura da colina e isso é tudo que precisa ser feito para construímos a aproximação quadrática. Também conhecida por Aproximação de Laplace, por ele ter utilizado o procedimento corretamente.

Fonte: wikipedia
Obs: No curso original, as estimativas são realizadas com a biblioteca Rethinking criadas e disponibilizadas pelo github do próprio professor Richard McElreath, pode ser acessado nesse endereço: https://github.com/rmcelreath/rethinking
A partir daqui iremos fazer em paralelo com o curso a utilização da biblioteca Stan-mc a página e a documentação oficial se encontram em Stan

Obs2: a estimativa da posteriori feita pela Stan utiliza algumas técnicas mais robustas do que a aproximação quadrática, porém no curso, essas estimativas são realizadas internamente na biblioteca rethinking e é invisível para o usuário, assim, o conteúdo dessas notas serão intimamente paralelas com o curso, sendo que se ocorrer um distanciamento entre ambas trajetórias, notas extras serão inseridas para minimizar esse longor.
import stan # Importando a Stan - estamos usando a pystan
# Essa estrutura está definida na página 77 - SR2
primeiro_codigo_stan = """
data {
int N;
real X[N];
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
X ~ normal(mu, sigma);
}
"""
mu_nao_observavel = 50
sigma_nao_observavel = 12
X = np.random.normal(mu_nao_observavel, sigma_nao_observavel, 1000) # Gerando os dados amostrais ~ Normal(50, 12)
meus_dados = {'N': len(X), 'X': list(X)} # Construíndo um dicionário com os dados
posteriori_model = stan.build(primeiro_codigo_stan, data=meus_dados) # Construíndo um modelo e anexando os dados
fit = posteriori_model.sample(num_chains=4, num_samples=1000) # Fazendo a amostragem da posteriori
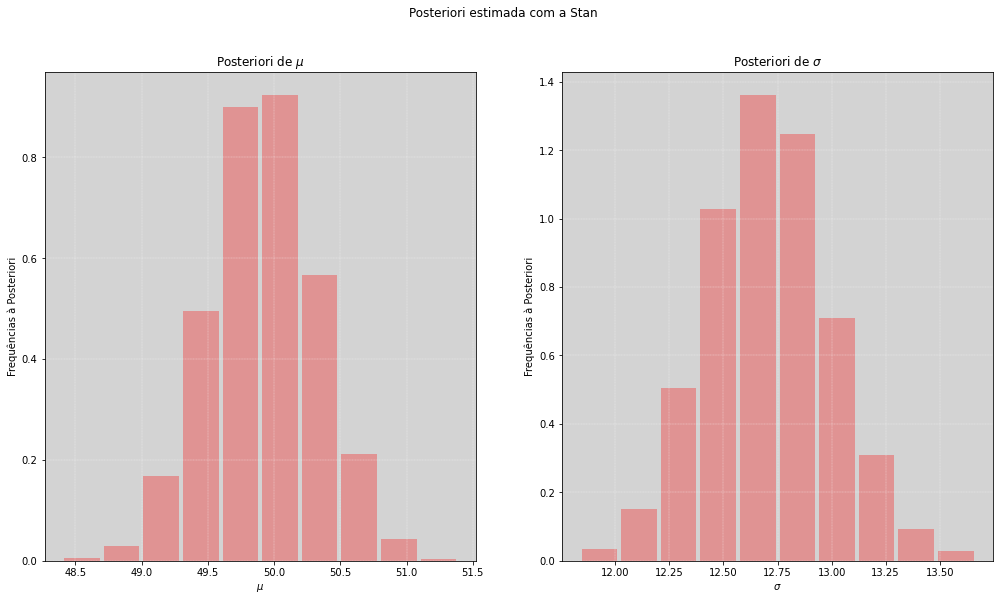
# Recuperando os parâmetros
mu_modelo_1 = fit['mu'].flatten() # Amostras da posteriori do 𝜇
sigma_modelo_1 = fit['sigma'].flatten() # Amostras da posteriori do 𝜎
print('='*70)
print(' mu médio: ', round(mu_modelo_1.mean(), 2), ' \t mu original: ', mu_nao_observavel)
print(' sigma médio: ', round(sigma_modelo_1.mean(), 2), ' \t sigma original: ', sigma_nao_observavel)
print('='*70)
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 9))
fig.suptitle("Posteriori estimada com a Stan")
ax1.hist(mu_modelo_1.flatten(), rwidth=0.9, density=True, color='red', alpha=0.3)
ax1.grid(color='white', ls='--', linewidth=0.3)
ax1.set_title('Posteriori de $\mu$')
ax1.set_xlabel('$\mu$')
ax1.set_ylabel('Frequências à Posteriori')
ax2.hist(sigma_modelo_1.flatten(), rwidth=0.9, density=True, color='red', alpha=0.3)
ax2.grid(color='white', ls='--', linewidth=0.3)
ax2.set_title('Posteriori de $\sigma$')
ax2.set_xlabel('$\sigma$')
ax2.set_ylabel('Frequências à Posteriori')
plt.show()
======================================================================
mu médio: 49.92 mu original: 50
sigma médio: 12.71 sigma original: 12
======================================================================
Estimando a altura usando a Stan¶
De volta ao exemplo anterior, vamos estimar a altura \(h\) usando um modelo escrito em Stan.
modelo_altura = """
data {
int N;
real altura[N];
}
parameters {
real mu;
real<lower=0, upper=50> sigma; // Priori para sigma ~ Uniform(0, 50)
}
model {
//mu ~ normal(178, 0.1); // *Teste com a priori muito informativa, veja o impacto do sigma à posteriori
//mu ~ normal(154, 0.1); // *Teste com a priori informativa com a média bem pŕoxima do que será estimado, usado apenas para entendimento, verifique que a média da variância se mantém.
mu ~ normal(178, 20); // Priori para mu
sigma ~ uniform(0, 50); // Priori para sigma
altura ~ normal(mu, sigma);
}
"""
altura = df.height.values
# Como recomenda a documentação https://mc-stan.org/docs/2_22/stan-users-guide/standardizing-predictors-and-outputs.html
# Iremos rescalonar o vetor de altura antes de mandar para a Stan
altura_media = altura.mean()
altura_std = altura.std()
altura_resc = (altura - altura_media) / altura_std
dados = {'N': len(altura),
'altura': altura} # Iremos usar a altura não normalizada para efeito de simplificação.
posteriori_model = stan.build(modelo_altura, data=dados)
fit_altura = posteriori_model.sample(num_chains=4, num_samples=1000)
# Compare o sigma usando duas priori diferentes para mu.
# (***) Com a priori mu ~ normal(178, 0.1), a posteriori do sigma tem um aumento significativo.
print('-'*40)
print('Média: ', np.mean(fit_altura['mu']))
print('Sigma: ', np.mean(fit_altura['sigma']))
print('-'*40)
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 5))
ax1.hist(fit_altura['mu'].flatten(), rwidth=0.9, density=True)
ax1.grid(color='white', ls='--', linewidth=0.3)
ax1.set_title('Posteriori $\mu$ da altura')
ax1.set_xlabel('Média do $\mu$ da altura (cm)')
ax2.hist(fit_altura['sigma'].flatten(), rwidth=0.9, density=True)
ax2.grid(color='white', ls='--', linewidth=0.3)
ax2.set_title('Posteriori $\sigma$ da altura')
ax2.set_xlabel('Média do $\sigma$ da altura')
plt.show()
----------------------------------------
Média: 154.60859753914997
Sigma: 7.774072031771385
----------------------------------------
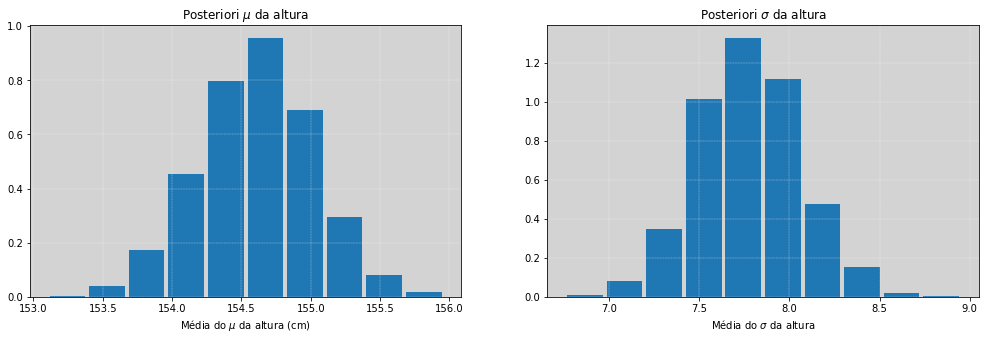
# =============================
# Modelo calculado na Stan
# =============================
# Recuperando os parâmetros
mu_altura = fit_altura['mu']
sigma_altura = fit_altura['sigma']
print('Comparativo com a amostra')
print('='*30)
print(' mu amostrado: ', round(df.height.mean(), 2))
print(' sigma amostrado: ', round(df.height.std(), 2))
print('='*30)
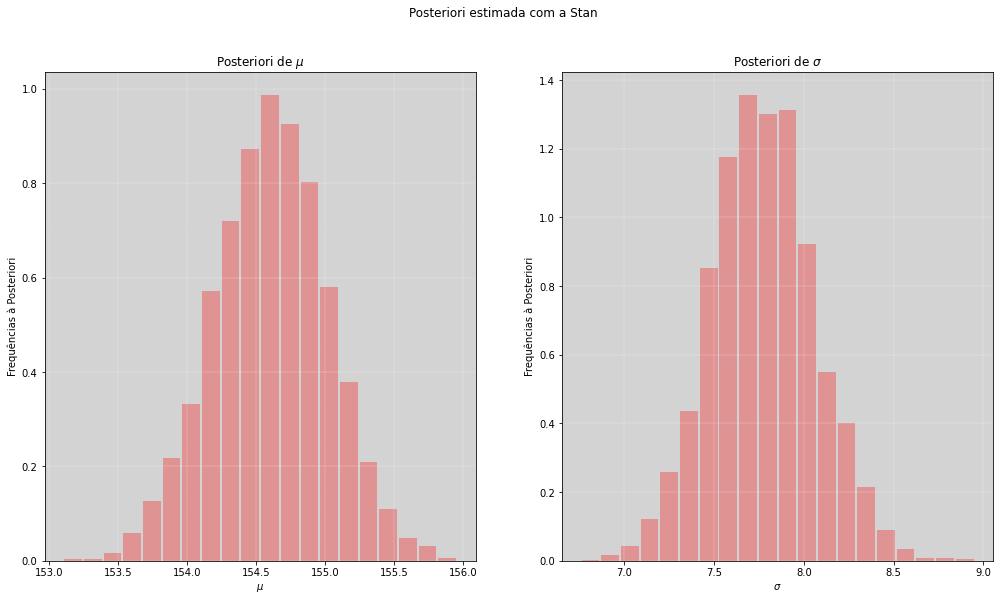
print(' mu médio: ', round(mu_altura.mean(), 2))
print(' sigma médio: ', round(sigma_altura.mean(), 2))
print('='*30)
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 9))
fig.suptitle("Posteriori estimada com a Stan")
ax1.hist(mu_altura.flatten(), bins=20, rwidth=0.9, density=True, color='red', alpha=0.3)
ax1.grid(color='white', ls='--', linewidth=0.3)
ax1.set_title('Posteriori de $\mu$')
ax1.set_xlabel('$\mu$')
ax1.set_ylabel('Frequências à Posteriori')
ax2.hist(sigma_altura.flatten(), bins=20, rwidth=0.9, density=True, color='red', alpha=0.3)
ax2.grid(color='white', ls='--', linewidth=0.3)
ax2.set_title('Posteriori de $\sigma$')
ax2.set_xlabel('$\sigma$')
ax2.set_ylabel('Frequências à Posteriori')
plt.show()
# =============================
# Modelo calculado na mão
# =============================
# Amostrando mu e sigma a partir da posteriori calculada na mão (exemplo construído acima)
amostras_posteriori_index = np.random.choice(np.arange(grid*grid), size=10000, replace=True, p=posteriori)
mu_amostrado = mu[amostras_posteriori_index]
sigma_amostrado = sigma[amostras_posteriori_index]
fig, [ax1, ax2] = plt.subplots(1, 2, figsize=(17, 9))
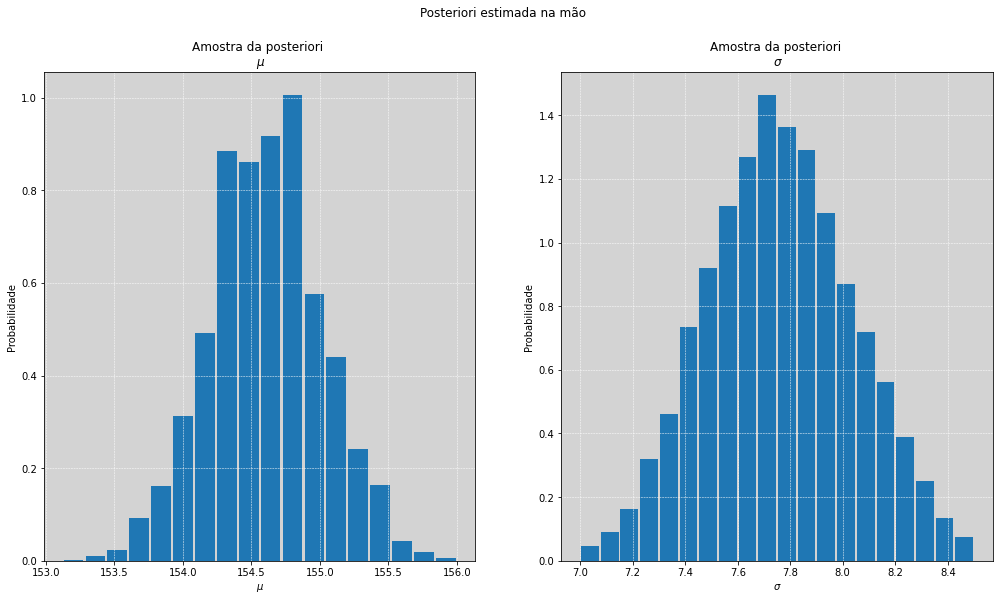
fig.suptitle("Posteriori estimada na mão")
ax1.hist(mu_amostrado, bins=18, rwidth=0.9, density=True)
ax1.set_title('Amostra da posteriori \n $\mu$')
ax1.set_xlabel('$\mu$')
ax1.set_ylabel('Probabilidade')
ax1.grid(color='white', ls='--', linewidth=0.5)
ax2.hist(sigma_amostrado, bins=20, rwidth=0.9, density=True)
ax2.set_title('Amostra da posteriori \n $\sigma$')
ax2.set_xlabel('$\sigma$')
ax2.set_ylabel('Probabilidade')
ax2.grid(color='white', ls='--', linewidth=0.5)
plt.show()
Comparativo com a amostra
==============================
mu amostrado: 154.6
sigma amostrado: 7.74
==============================
mu médio: 154.61
sigma médio: 7.77
==============================
Adicionando uma variável Preditora¶
Agora, iremos refazer a estimativa da altura, mas iremos usar mais uma variável para nos ajudar explicar melhor a altura, e assim teremos mais informações. Usaremos a variável peso (weight) que nos ajudará a entender melhor a altura (height)?
Obs: Iremos selecionar apenas as pessoas que tenham acima de 18 anos de idade para todos os estudo a seguir.
# Gráfico de dispersão - peso ajudar a identificar qual a altura.
plt.figure(figsize=(17, 9))
plt.scatter(df.loc[df.age >= 18, 'weight'], # Filtro para todos as pessoas que tem acima de 18 anos
df.loc[df.age >= 18, 'height']) # Filtro para todos as pessoas que tem acima de 18 anos
plt.title('Gráfico de Dispersão')
plt.xlabel('Peso (weight)')
plt.ylabel('Altura (height)')
plt.grid(color='white', ls='--', linewidth=0.4)
plt.show()
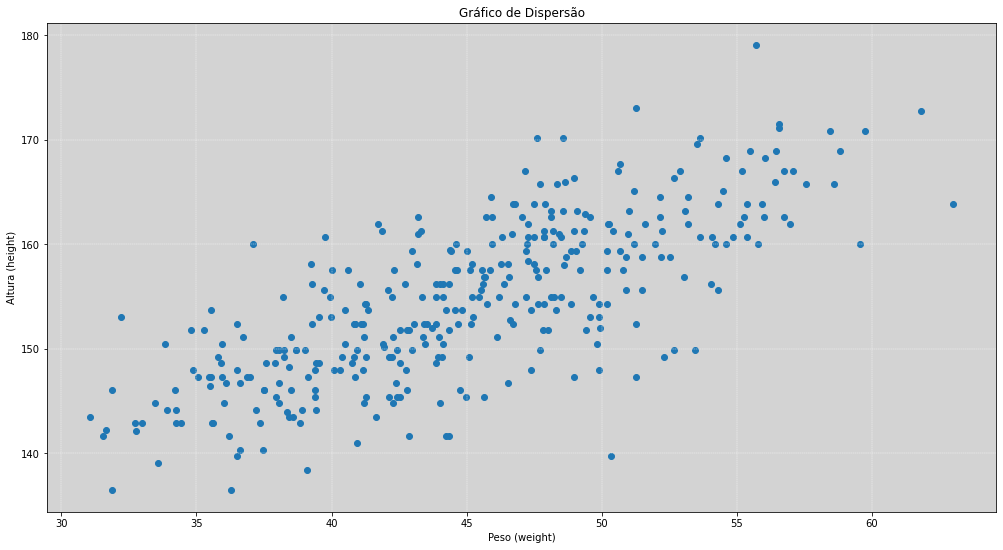
Usando um modelo linear de média, \(\mu\):
Vamos agora construir uma reta, um modelo linear. Até agora nós fizemos inferências de \(1\) ou \(2\) parâmetros e que podem ser aproximadas como uma gaussiana.
Mas o que significa fazer um modelo linear, ou utilizar uma reta no modelo? Isso significa que podemos adicionar uma nova variável que irá nos ajudar a melhorar nosso entendimento da variável altura. Essa nova variável terá a função, dentro do nosso modelo, de predizer, ou seja, dizer antecipadamente, antever, adivinhar, prever qual é a da altura do indivíduo, probabilisticamente. Chamamos todas essas variáveis que podem nos ajudar de variáveis preditoras.
A principal ideia em adicionar uma variável preditora, assim como outras variáveis do nosso conjunto de dados, é que quando aprendemos, podemos fazer melhores previsões sobre o resultado de interesse que, nesse caso, é a altura.
Para ficar mais claro, quando pretendemos saber a altura de uma pessoa sem termos nenhuma informação adicional, o melhor que podemos fazer é usar a estimativa da altura da população toda para estimar a altura desse indivíduo. É o máximo que podemos fazer com as informações que temos disponíveis.
Mas se esse mesmo indivíduo, assim como todos da amostra, nos informar uma característica a mais para nós estimarmos sua altura? Nesse exemplo, o peso é uma dessas informações adicionais, variável preditora, assim teremos mais conhecimento para poder estimar a sua altura.
Explicando o modelo acima:¶
Agora temos que \(h_i\) também contínua distribuída como uma Gaussiana como no exemplo anterior, porém agora a média \(\mu\) não é apenas distribuída normalmente com a média fixa em 178, dependerá de cada indivíduo \(i\), assim:
\(x_i\) representa o peso de uma pessoa em particular.
Em instante iremos entender melhor o que significa todos os termos de \(\mu\). O \(\alpha\) e o \(\sigma\) continuam com as mesmas prioris do exemplo anterior, e agora temos uma nova distribuição à priori para \(\beta\), que é o responsável por descrever a relação entre altura e o peso.
Observando mais profundamente a estrutura que criamos nosso novo modelo:
\(\mu_i\) = é a média da linha i
\(\alpha\) = é a altura média da quando \(x_i = \bar{x}\), conhecida como o
intercepto. (Lindo!!!)\(\beta\) = taxa de mudança para \(\mu\) cada unidade de mudança de \(x_i\), conhecido como a
inclinação.
Se por acaso o \(\beta\) for zero, estamos novamente no modelo anterior. Ou seja, estamos dizendo que não há relação transmitida para o \(\mu\) a partir do peso. Do contrário, cada número que o \(x_i\) sobe, subimos \(\beta\) o \(\mu\).
Escrever nossos modelos lineares dessa forma nos permite entender e definir melhor os parâmetros e nossa prioris, mas nem todos os modelos devem ser escritos dessa forma e nesse caso deveremos ter uma boa justificativa.
Distribuição Priori Preditiva¶
Quais são as prioris desse modelo e o que essas prioris significam?
Como, no exemplo anterior, vamos simular para entender e compreender as implicações do modelo.
# ===========================
# Simulando a Priori
# ===========================
N = 100 # A quantidade de vezes que iremos simular os dados da priori
alpha_priori = np.random.normal(178, 20, N)
beta_priori = np.random.normal(0, 10, N)
plt.figure(figsize=(17, 9))
for i in range(N):
plt.plot(np.linspace(30, 65, N),
alpha_priori[i] + beta_priori[i] * (np.linspace(-17.5, 17.5, N)), # (x_i - x_bar)
color='blue', linewidth=0.2)
plt.ylim(-100, 400)
plt.hlines(0, 30, 65, ls='--', color='red', alpha=0.8) # Linha inferior vermelha: Altura óvulo fertilizado (0cm)
plt.hlines(272, 30, 65, ls='--', color='red', alpha=0.8) # Linha superior vermelha: Pessoa mais alta do mundo (272 cm)
plt.annotate('Pessoa mais alta já registrada \n (272 cm)', (44, 280), color='red')
plt.annotate('Altura do Embrião \n (0 cm)', (43, -25), color='red')
plt.title('Priori: $alpha + beta * x_i$')
plt.ylabel('Altura $h_i$')
plt.xlabel('Peso $x_i$')
plt.grid(color='white', ls='--', linewidth=0.4)
plt.show()
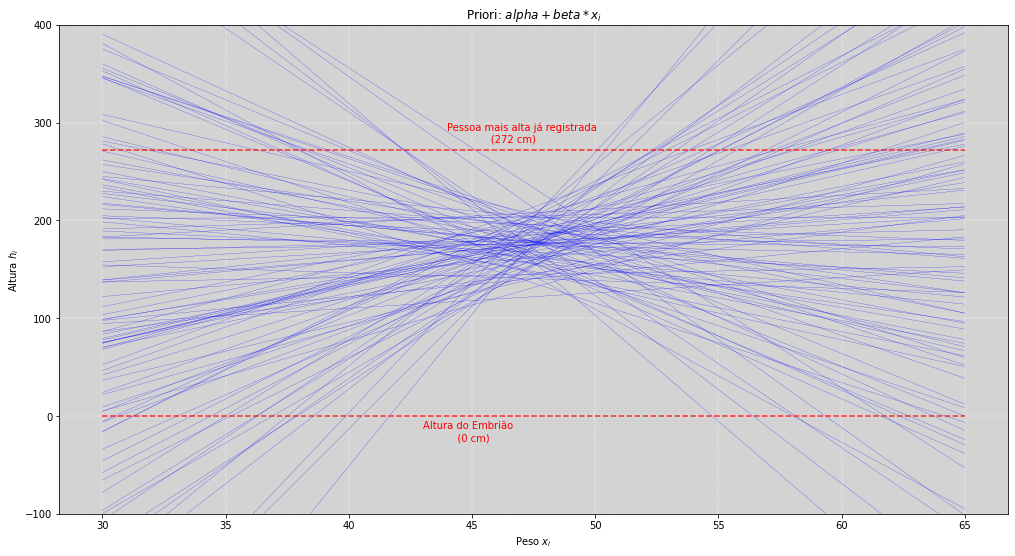
O resultado das simulações da distribuição à priori do \(\alpha\) e o \(\beta\), geram as curvas acima, de acordo o modelo:
com podemos ver no gráfico, muitas linhas tem valores superiores à altura de \(272 cm\). Também podemos ver que existem linhas que indicam alturas menores que zero, o que naturalmente deveria estar errado. Ambos comportamentos são prioritariamente resultantes dos valores gerados pela distribuição dos \(\beta\)’s, a inclinação da reta.
Note
Essas retas são as nossas crenças à priori.
Agora que temos um pouco mais de intimidade com o comportamento das nossas prioris, podemos concluir que devemos diminuir nosso entusiasmo com relação ao \(\beta\), pois essa é uma priori muito ruim. Haverá momentos, em situações reais, que será necessário verificar a compatibilidade com o mundo real. Faça alterações nas prioris para verificar a mudança no efeito.
Distribuição Preditiva da Priori¶
Nós agora sabemos algo sobre as prioris, temos um conhecimento científico sobre a nossa distribuição dos \(\beta\)’s, sabemos que ele é positivo, assim, então, vamos transforma-lo em positivo?
Mas como?
Para fazer isso, usaremos a distribuição log-Normal. Essa distribuição pode ser um pouco menos conhecida, porém é muito útil para situações desse tipo. Essa distribuição, log-Normal, construída partir da exponenciação dos valores da distribuição Normal.
Na teoria das probabilidades, uma distribuição log-normal (ou lognormal) é uma distribuição de probabilidade contínua de uma variável aleatória cujo logaritmo é normalmente distribuído.
Assim, se a variável aleatória \(X\) é log-normalmente distribuída, então \(Y = log(X)\) tem uma distribuição normal. (Ref. Wikipedia)
Referências:
Um caminho para se entender melhor o que é uma \(lognormal\) é o seguinte:
Qual é a distribuição de \(X\), na qual, ao aplicarmos o log, \(log(X)\), ela se tornará \(Normal\)? Naturalmente temos que:
de acordo com a expressão abaixo:
se a distribuição de \(X\) for:
então a operação abaixo é válida,
logo,
então, assim teremos que:
# =====================================
# Estudos sobre as Log-Normais
# =====================================
# Iremos plotar, a partir de uma
# distribuição normal, uma lognormal
# e compara-la com amostragem da
# lognormal implementada no Numpy!
# =====================================
d_normal = np.random.normal(0, 1, 1000)
d_lognormal = np.random.lognormal(0, 1, 1000)
fig, [[ax1, ax2],[ax3, ax4]] = plt.subplots(2, 2, figsize=(17, 9))
ax1.hist(np.exp(d_normal), bins=150, density=True, rwidth=0.8)
ax1.set_title('$exp( Normal(0,1) )$ \n Log Normal gerada na mão')
ax1.grid(color='white', ls='--', linewidth=0.4)
ax2.hist(d_lognormal, bins=150, density=True, rwidth=0.8)
ax2.set_title('Histograma da distribuição lognormal \n Gerada usando Numpy')
ax2.grid(color='white', ls='--', linewidth=0.4)
ax3.hist(np.exp(d_normal), bins=150, density=True, rwidth=0.8)
ax3.set_xlim(0, 5)
ax3.set_title('$exp( Normal(0,1) )$ \n Log Normal gerada na mão \n Mostrando valores de 0 a 5')
ax3.grid(color='white', ls='--', linewidth=0.4)
ax4.hist(d_lognormal, bins=250, density=True, rwidth=0.8)
ax4.set_xlim(0, 5)
ax4.set_title('Histograma da distribuição lognormal \n Gerada usando Numpy \n Mostrando os valores de 0 a 5')
ax4.grid(color='white', ls='--', linewidth=0.4)
plt.tight_layout() # Ajustar as distâncias entre os gráficos
plt.show()
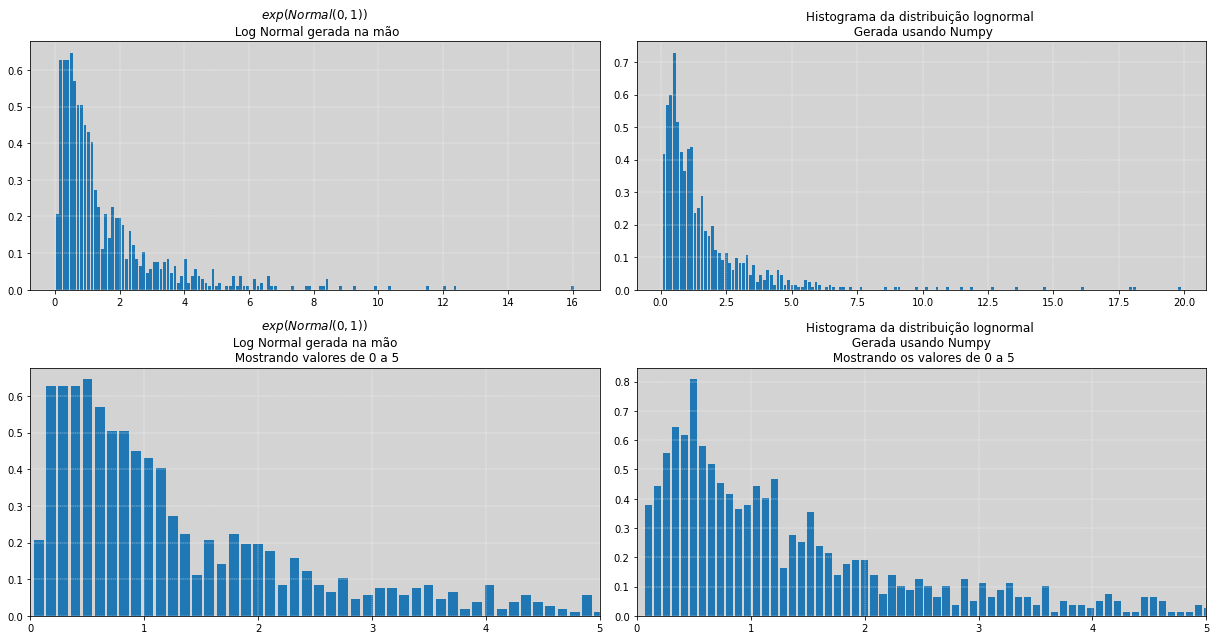
Com a lognormal explicada, iremos trocar a distribuição da a priori de:
para uma priori que é distribuída conforme uma lognormal:
Assim, como antes, vamos simular para entender o novo comportamento da nossa priori.
# ==========================================
# Simulando a priori com log-normal
# ==========================================
N = 100 # A quantidade de vezes que iremos simular os dados da priori
alpha_priori = np.random.normal(178, 20, N)
beta_priori = np.random.lognormal(0, 1, N) # Priori lognormal(0, 1)
plt.figure(figsize=(17, 9))
for i in range(N):
plt.plot(np.linspace(30, 65, N), alpha_priori[i] + beta_priori[i] * (np.linspace(-17.5, 17.5, N)), # (x_i - x_bar)
color='blue', linewidth=0.1)
plt.ylim(-100, 400)
plt.hlines(0, 30, 65, ls='--', color='red', alpha=0.8) # Linha inferior vermelha: Altura óvulo fertilizado (0cm)
plt.hlines(272, 30, 65, ls='--', color='red', alpha=0.8) # Linha superior vermelha: Pessoa mais alta do mundo (272 cm)
plt.annotate('Pessoa mais alta já registrada \n (272 cm)', (43, 280), color='red')
plt.annotate('Altura do Embrião \n (0 cm)', (43, -25), color='red')
plt.title('Priori: $alpha + beta * x_i$')
plt.ylabel('Altura $h_i$')
plt.xlabel('Peso $x_i$')
plt.grid(color='white', ls='--', linewidth=0.4)
plt.show()
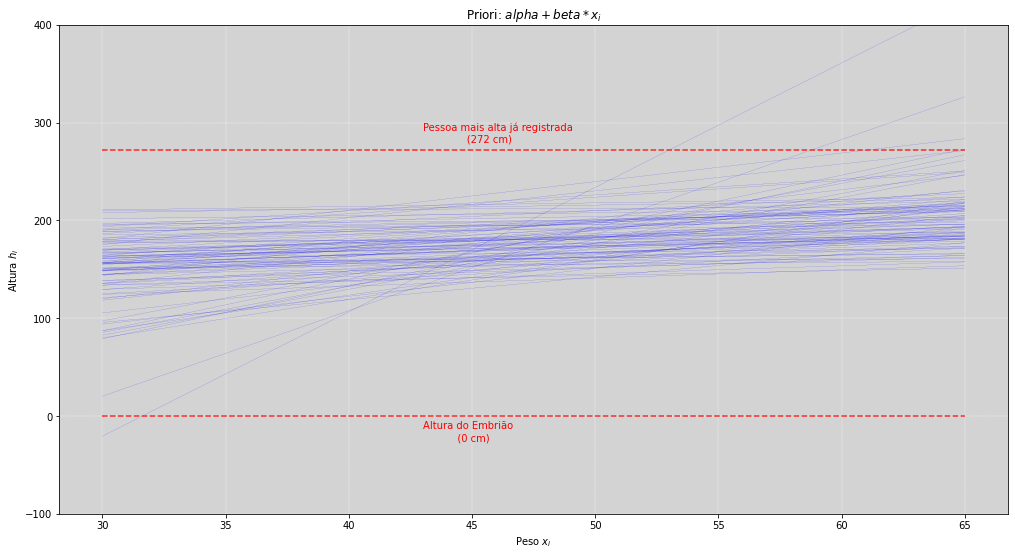
Nós ainda temos muita dispersão e também temos ainda algumas poucas linhas que ultrapassam a maior altura já registrada (de \(272 cm\)). Isso acontece porque não limitamos a nossa margem superior pela distribuição de \(\beta\). Mas essa nossa nova abordagem parece ser uma priori bem mais condizente com o que podemos imaginar.
Aproximação da posteriori¶
Vamos fazer a aproximação da posteriori usando a Stan e verificar os resultados.
# =================================================================
# Aproximando a posteriori da altura usando o peso da pessoa
# =================================================================
modelo_altura_2 = """
data {
int N;
real x_barra;
real altura[N];
real peso[N];
}
parameters {
real alpha;
real<lower=0> beta;
real<lower=0, upper=50> sigma;
}
model {
alpha ~ normal(178, 20);
beta ~ lognormal(0, 1);
// sigma ~ uniform(0, 50);
for (i in 1:N){
altura[i] ~ normal(alpha + beta * (peso[i] - x_barra), sigma);
}
}
"""
# Nossa amostra é apenas para pessoas acima de 18 anos
df_maioridade = df.loc[df.age >= 18, ['weight', 'height']]
# Definindo as variáveis
N = len(df_maioridade)
x_barra = df_maioridade.weight.mean()
altura = df_maioridade.height.values
peso = df_maioridade.weight.values
# Construindo o dicionário
meus_dados_2 = {'N': N,
'x_barra': x_barra,
'altura': altura,
'peso': peso}
# Rodando o modelo
posteriori_model_2 = stan.build(modelo_altura_2, data=meus_dados_2)
fit_altura_2 = posteriori_model_2.sample(num_chains=4, num_samples=1000)
# =============================
# Modelo calculado na Stan
# =============================
# Recuperando os parâmetros
alpha_posteriori = fit_altura_2['alpha'].flatten()
beta_posteriori = fit_altura_2['beta'].flatten()
print('Resumo das posterioris:')
print('='*60)
print('Media alpha: ', round(fit_altura_2['alpha'].mean(), 1),
' - Desvio Padrão alpha: ', round(fit_altura_2['alpha'].std(), 3))
print('Média beta: ', round(fit_altura_2['beta'].mean(), 3),
' - Desvio Padrão beta: ', round(fit_altura_2['beta'].std(), 3))
print('Média sigma: ', round(fit_altura_2['sigma'].mean(), 3),
' - Desvio Padrão sigma: ', round(fit_altura_2['sigma'].std(), 3))
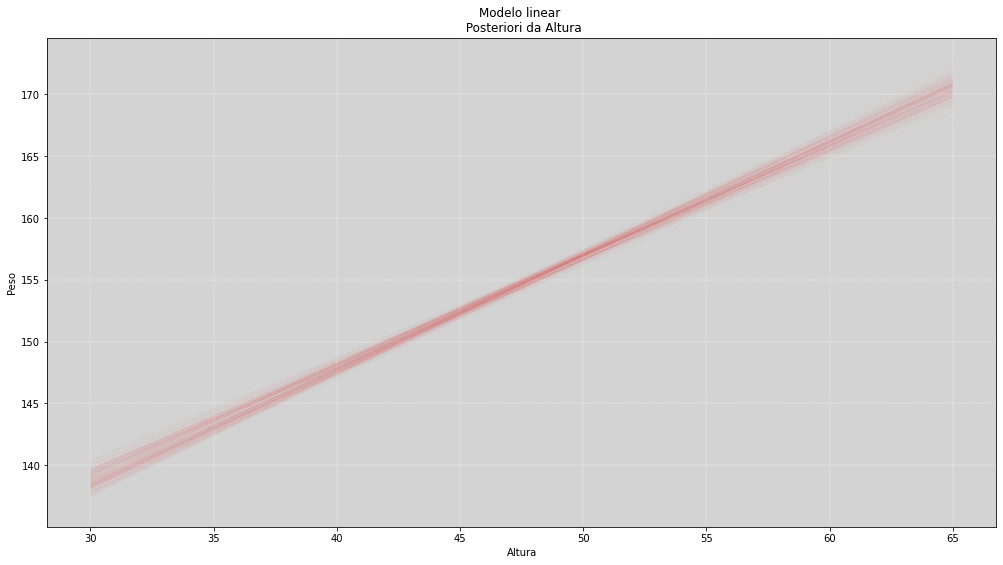
N = len(alpha_posteriori) # Plotar todas as curvas estimadas
N = 200 # Plotar as 200 primeiras curvas
plt.figure(figsize=(17, 9))
plt.title('Modelo linear \n Posteriori da Altura')
plt.xlabel('Altura')
plt.ylabel('Peso')
for i in range(N):
plt.plot(np.linspace(30, 65, N), alpha_posteriori[i] + beta_posteriori[i] * (np.linspace(-17.5, 17.5, N)),
color='red', linewidth=0.01)
plt.grid(color='white', ls='--', linewidth=0.4)
plt.show()
# ==========================================
# Plot todas as variáveis estimadas
# ==========================================
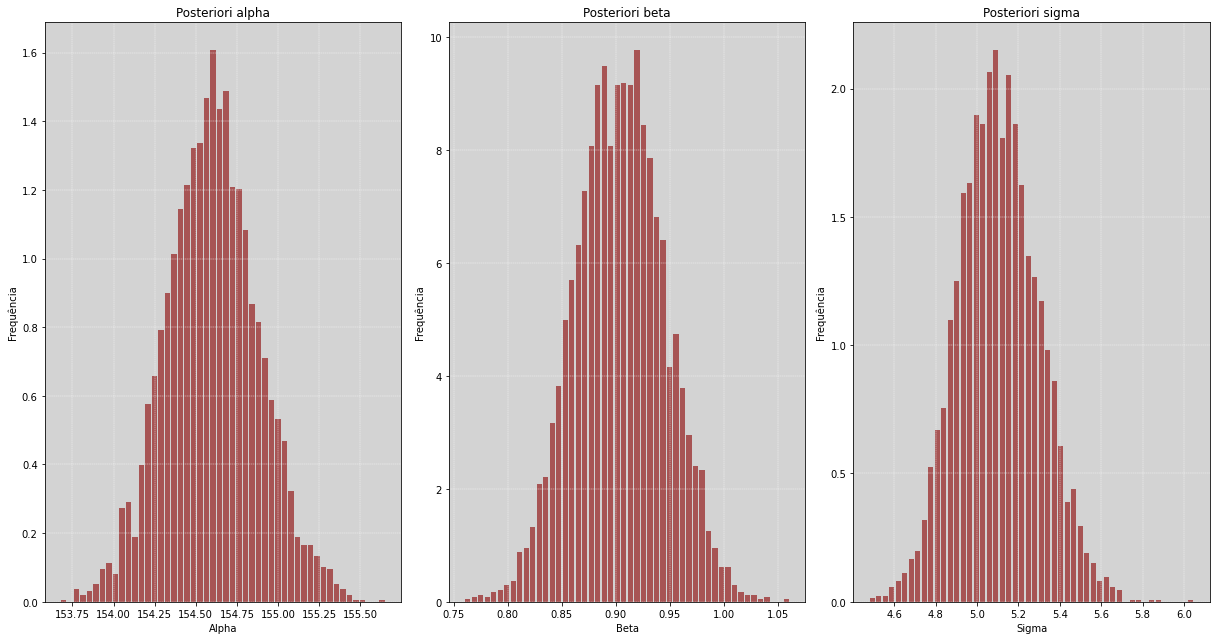
fig, [ax1, ax2, ax3] = plt.subplots(1, 3, figsize=(17, 9))
ax1.hist(fit_altura_2['alpha'].flatten(), bins=50, density=True, rwidth=0.8, color='darkred', alpha=0.6)
ax1.set_title('Posteriori alpha')
ax1.grid(color='white', ls='--', linewidth=0.4)
ax1.set_ylabel('Frequência')
ax1.set_xlabel('Alpha')
ax2.hist(fit_altura_2['beta'].flatten(), bins=50, density=True, rwidth=0.8, color='darkred', alpha=0.6)
ax2.set_title('Posteriori beta')
ax2.grid(color='white', ls='--', linewidth=0.4)
ax2.set_ylabel('Frequência')
ax2.set_xlabel('Beta')
ax3.hist(fit_altura_2['sigma'].flatten(), bins=50, density=True, rwidth=0.8, color='darkred', alpha=0.6)
ax3.set_title('Posteriori sigma')
ax3.grid(color='white', ls='--', linewidth=0.4)
ax3.set_ylabel('Frequência')
ax3.set_xlabel('Sigma')
plt.tight_layout() # Ajustar as distâncias entre os gráficos
plt.show()
Resumo das posterioris:
============================================================
Media alpha: 154.6 - Desvio Padrão alpha: 0.278
Média beta: 0.904 - Desvio Padrão beta: 0.041
Média sigma: 5.105 - Desvio Padrão sigma: 0.195
Resumo¶
Até aqui vimos a construção de um modelo linear simples usando a Stan, vimos também como pensar e como construir uma priori, vimos como gerar as amostras da posteriori e analisar seus resultados.
O modelo linear é o modelo muito simples e é empregado em muitas análises no dia a dia.
Na mesma linha de raciocínio que usamos para pensar e construir esse modelo de regressão linear, nós também iremos utilizá-la na próxima parte desse material. Iremos adicionar mais ferramentas dentro dessa estrutura e, com isso, aumentaremos um pouco mais a profundidade que nossas análises podem alcançar.